Jean-François Marckert: Ladder Variables, Internal Structure of Simple Trees and Finite Branching Random Walks

This is a joint work with Abdelkader Mokkadem.

We consider Galton-Watson branching process with offspring $N$, starting with 1 individual in generation 0. $N$ is a non-negative, integer-valued random variable with mean 1 and variance $\sigma^2$. We note $(p_i)_{i\geq 0}=({\bf P}(N=i))_{i\geq 0}$ the offspring distribution.

We write $\zeta$ for the family tree of this branching process and $\Omega$ the probability space of all trees with the law induced by $N$. We note $\Omega_n$ the space of size $n$ trees endowed by the conditional law given $\vert\zeta\vert=n$ (under this condition, Galton-Watson trees are simple trees). The law on $\Omega_n$ will be denoted by ${\bf P}_n$.

Let $u$ be a node of $\zeta$ and note $a_k(u)$ the number of ancestors of $u$ ($u$ excluded) that have $k$ children. We note $h(u)$ the depth of the node $u$ (that is $h(u)=d(u,root)$).

We ``show'' strong and uniform properties of the random variables $a_k(u)$:

Theorem Let $\beta$ be a positive real number.

For any $\gamma>\sqrt{(\beta+4)\sqrt{(\beta+7/2) g}/2},$

$${\bf P}_n\Big(\sup_{u\in\zeta, k}\big\vert a_k(u)-kp_k h(u) \big\vert> \gamma n^{1/4}\ln n\Big)=o(n^{-\beta}).$$

That is, $a_k(u)$ is roughly speaking proportional to $h(u)$, and this ``uniformly'' in $u$.

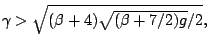
To obtain this result (and other ones), we derive properties of ladder variables (the ladder variables are the random variables that intervene in the records of a random walk: time of the records, values of the record, increment that gives a record).

Application to moderate deviations of finite branching random walk are also given.

Back to the Index