A 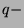 multiplicative function is an unimodular sequence
multiplicative function is an unimodular sequence 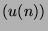 satisfying the conditions
satisfying the conditions
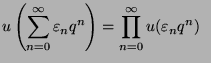
and
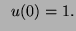
A classical object related to the sequence 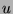 is the dynamical system
is the dynamical system
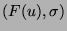 ,
where
,
where 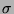 is the shift operator and
is the shift operator and 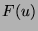 the closed orbit of
the closed orbit of 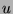 under its action.
We study the structure of this dynamical system and especially give conditions under
which it is minimal and/or ergodic. The case of
under its action.
We study the structure of this dynamical system and especially give conditions under
which it is minimal and/or ergodic. The case of 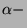 multiplicative functions
(which is the natural analogon w.r.t. Ostrowski's systems of numeration) is also investigated.
The main tools are skew products, essential values in the sense of Klaus Schmidt and appropriate
compactifications of the set of the natural integers (odometers). Previous results of Liardet,
Lesigne, and Mauduit are retrieved and extended.
multiplicative functions
(which is the natural analogon w.r.t. Ostrowski's systems of numeration) is also investigated.
The main tools are skew products, essential values in the sense of Klaus Schmidt and appropriate
compactifications of the set of the natural integers (odometers). Previous results of Liardet,
Lesigne, and Mauduit are retrieved and extended.
- 1
-
Guy Barat and Pierre Liardet.
Dynamical systems originated in the ostrowski alpha-expansion.
(to appear in Publ. Math. Debrecen).
- 2
-
Emmanuel Lesigne, Christian Mauduit, and Brigitte Mossé.
Le théorème ergodique le long d'une suite 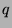 -multiplicative.
-multiplicative.
Compositio Math., 93(1):49-79, 1994.
- 3
-
Klaus Schmidt.
Cocycles on ergodic transformation groups.
Macmillan Company of India, Ltd., Delhi, 1977.
Macmillan Lectures in Mathematics, Vol. 1.
Back to the Index
Please send comments and corrections to Thomas Klausner.
![]() multiplicative function is an unimodular sequence
multiplicative function is an unimodular sequence ![]() satisfying the conditions
satisfying the conditions
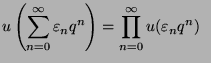 and
and