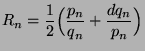Let  be a positive integer which is not a perfect square.
Let
be a positive integer which is not a perfect square.
Let  denote the
denote the 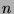 -th convergent and
-th convergent and 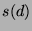 the length
of the shortest period in the simple continued fraction expansion
of
the length
of the shortest period in the simple continued fraction expansion
of 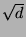 .
It was proved by Mikusinski in 1954 that if
.
It was proved by Mikusinski in 1954 that if
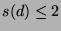 ,
then all Newton's approximants
,
then all Newton's approximants
are convergents of 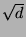 , and moreover
, and moreover
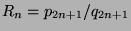 for all nonegative integers
for all nonegative integers 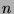 .
If
.
If 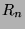 is a convergent of
is a convergent of 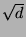 , then we say that
, then we say that 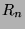 is a
"good approximant". In 2001, we proved the converse of Mikusinski's
result, namely that if all approximants are good, then
is a
"good approximant". In 2001, we proved the converse of Mikusinski's
result, namely that if all approximants are good, then
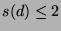 .
It is easy to see that
.
It is easy to see that
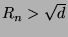 . Therefore, good approximants
satisfy
. Therefore, good approximants
satisfy
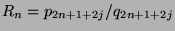 for an integer
for an integer 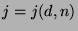 .
If
.
If
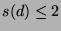 , then
, then
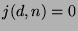 . For
. For 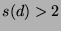 ,
we proved the upper bound
,
we proved the upper bound
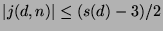 , and we presented a sequence of
, and we presented a sequence of 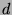 's
(given in terms of Fibonacci numbers) which shows that this
upper bound for
's
(given in terms of Fibonacci numbers) which shows that this
upper bound for 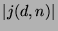 is sharp.
Let
is sharp.
Let 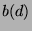 denote the number of good approximants among the numbers
denote the number of good approximants among the numbers
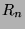 ,
,
 . We will present some results and
conjectures (based on experimental data) about the magnitude of
. We will present some results and
conjectures (based on experimental data) about the magnitude of 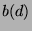 compared with
compared with 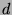 and
and 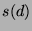 .
.
Back to the Index
Please send comments and corrections to Thomas Klausner.
![]() be a positive integer which is not a perfect square.
Let
be a positive integer which is not a perfect square.
Let ![]() denote the
denote the ![]() -th convergent and
-th convergent and ![]() the length
of the shortest period in the simple continued fraction expansion
of
the length
of the shortest period in the simple continued fraction expansion
of ![]() .
It was proved by Mikusinski in 1954 that if
.
It was proved by Mikusinski in 1954 that if
![]() ,
then all Newton's approximants
,
then all Newton's approximants