Let 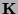 be an algebraically closed field of characteristic 0,
be an algebraically closed field of characteristic 0,
![$ P(X) \in {\bf K}[X]$](Pethoe-img4.png) and
and
![$ Q(X,Y) \in {\bf K}[X,Y]$](Pethoe-img5.png) . Let further
. Let further
![$ A_0,\dots,A_{d-1},G_0,\dots,G_{d-1} \in {\bf K}[X]$](Pethoe-img6.png) and the sequence of
polynomials
and the sequence of
polynomials
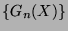 be defined by the recursion
be defined by the recursion
for all 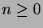 .
.
In this talk we are given a survey on results concerning the equation
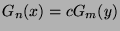 |
(1) |
in integers 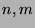 with
with 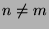 , where
, where
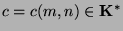 . We assume
that
. We assume
that 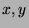 are transcendental over
are transcendental over 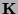 , but algebraically dependent,
i.e.
, but algebraically dependent,
i.e.
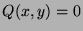 holds. Our journey is based on joint works with Cl. Fuchs
and R.F. Tichy as well as on a paper of U. Zannier. If
holds. Our journey is based on joint works with Cl. Fuchs
and R.F. Tichy as well as on a paper of U. Zannier. If
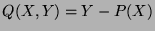 then (1) has up to two exceptional families only finitely
many solutions and Zannier proved a quite good bound for the number of
solutions. In the general case we have also a quite satisfactory
description of the exceptional cases.
then (1) has up to two exceptional families only finitely
many solutions and Zannier proved a quite good bound for the number of
solutions. In the general case we have also a quite satisfactory
description of the exceptional cases.
We finish our talk by some open problem.
Back to the Index
Please send comments and corrections to Thomas Klausner.
![]() be an algebraically closed field of characteristic 0,
be an algebraically closed field of characteristic 0,
![]() and
and
![]() . Let further
. Let further
![]() and the sequence of
polynomials
and the sequence of
polynomials
![]() be defined by the recursion
be defined by the recursion