Let 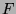 be a finite field and
be a finite field and
with
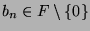 .
We define a new kind of digit system in the quotient ring
.
We define a new kind of digit system in the quotient ring
![$ {F}[x,y]/p(x,y){F}[x,y]$](Scheicher-img4.png) .
There are striking analogies of these digit systems to the well
known canonical number systems (CNS) defined in
.
There are striking analogies of these digit systems to the well
known canonical number systems (CNS) defined in
![$ Z[x]/P(x)Z[x]$](Scheicher-img5.png) for a polynomial
for a polynomial
![$ P(x)\in Z[x]$](Scheicher-img6.png) .
Especially, the problem of characterizing the possible bases is solved.
In contrast, such a characterization for CNS is still outstanding.
Furthermore, we will study
.
Especially, the problem of characterizing the possible bases is solved.
In contrast, such a characterization for CNS is still outstanding.
Furthermore, we will study 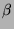 -expansions in
-expansions in
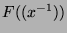 ,
the field of formal Laurent series over
,
the field of formal Laurent series over 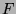 in the variable
in the variable 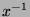 . Once again,
we can solve problems corresponding to open problems on classical
. Once again,
we can solve problems corresponding to open problems on classical
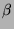 -expansions.
-expansions.
Back to the Index
Please send comments and corrections to Thomas Klausner.
![]() be a finite field and
be a finite field and
![$\displaystyle p(x,y)=\sum_{j=0}^n b_j(x)y^j\in {F}[x,y]$](Scheicher-img2.png)