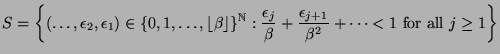Let 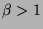 be a real number and
be a real number and
be the set of all (inversed) greedy expansions in base 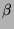 .
Then the
.
Then the 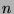 -th element of the generalised van der Corput sequence in base
-th element of the generalised van der Corput sequence in base 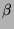 is defined by the
is defined by the 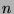 -th element of
-th element of 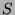 with respect to the
lexicographical order,
with respect to the
lexicographical order,
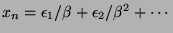 .
If the expansion of 1 in base
.
If the expansion of 1 in base 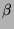 is finite or ultimately periodic, then we
have a substitution such that the digits of
is finite or ultimately periodic, then we
have a substitution such that the digits of 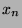 are the lengths of the words in the
expansion of
are the lengths of the words in the
expansion of 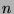 with respect to this substitution.
This allows us to get explicit formulae for the local discrepancy (
with respect to this substitution.
This allows us to get explicit formulae for the local discrepancy (
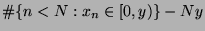 ) of the sequence.
If
) of the sequence.
If 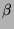 is a Pisot number and the
is a Pisot number and the 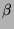 -polynomial is the minimal polynomial of
-polynomial is the minimal polynomial of 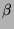 ,
then the local discrepancy is bounded (in
,
then the local discrepancy is bounded (in 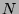 ) if and only if either the
) if and only if either the 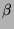 -expansion
of
-expansion
of 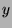 is finite or its tail is the same as the tail of the expansion of 1.
is finite or its tail is the same as the tail of the expansion of 1.
Back to the Index
Please send comments and corrections to Thomas Klausner.
![]() be a real number and
be a real number and