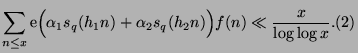This is an account on two joint works with Cécile Dartyge (Nancy 1).
Let
While a fairly simple proof of (1) may be provided when ![]() , the
general case requires rather sophisticated
tools. The approach followed in the above-mentioned works is based
on an upper bound for the quantity
, the
general case requires rather sophisticated
tools. The approach followed in the above-mentioned works is based
on an upper bound for the quantity
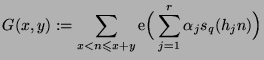
Other applications of this general device will be described, in particular the following two, where congruence properties of sums of digits may be combined with multiplicative constraints.
(i) Given positive integers
![]() with
with
![]() ,
,
![]() ,
, ![]() ,
there exist infinitely many integers
,
there exist infinitely many integers ![]() having exactly
having exactly ![]() prime
factors and such that
prime
factors and such that
![]() . This improves on a result of
Étienne Fouvry and Christian Mauduit by removing an indetermination
arising from the so-called parity
phenomenon.
. This improves on a result of
Étienne Fouvry and Christian Mauduit by removing an indetermination
arising from the so-called parity
phenomenon.
(ii) Daboussi-type theorem for sums of digits.
Let
![]() ,
,
![]() , and
, and
![]() .
Uniformly for
.
Uniformly for