Aufgabe: Konstruiere in einem Punkt Q eines Kegelschnitts die Tangenten als Winkelsymmetrale der Brennstrahlen.
Aufgabe: Konstruiere in einem Punkt Q eines Kegelschnitts die Tangenten mit Hilfe des Leit- oder Gegenpunktkreises.
Aufgabe:
Zeichne in einem Punkt Q einer Ellipse (Hyperbel, Parabel) die Kegelschnittstangente
t und schneide diese mit der zu t normalen Geraden durch einen
Brennpunkt. Untersuche die Ortslinie des Schnittpunktes, wenn sich der Punkt
Q auf dem Kegelschnitt bewegt (Fußpunktkurve).
Gib an, wie diese Eigenschaft ebenfalls zur Konstruktion einer Kegelschnittstangente
herangezogen werden kann.
Aufgabe: Satz von Archimedes: Verkürzt oder verlängert man die zu einem Kreisdurchmesser normalen Sehnen in einem konstanten Verhältnis, so erhält man eine Ellipse.
Aufgabe:
Satz von Pappos-Pascal: Werden auf einem Kegelschnitt sechs
Punkte 1,2,3,4,5,6 ausgewählt, so gilt: die Schnittpunkte der Geraden
1,2 und 4,5 bzw. 2,3 und 5,6 bzw. 3,4 und
6,1 liegen auf einer Geraden. Dies kann ebenfalls zur Konstruktion eines
Kegelschnitts verwendet werden.
Bemerkung: Dieser Satz gilt selbstverständlich auch für Kreise sowie
für ein Geradenpaar, wobei je drei Punkte auf einer Geraden gewählt
werden.
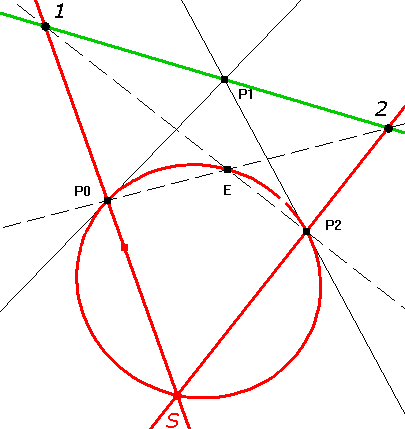
Aufgabe: Erzeugung nach Krüger (vgl. Havlicek): Gegeben sind zwei Punkte P0 und P2 eines Kegelschnitts k samt ihren Tangenten, sowie ein weiterer Punkt E von k. Der Schnittpunkt der beiden Tangenten sei mit P1 bezeichnet. Wählt man nun auf der Geraden P2,E einen beliebigen Hilfspunkt 1, so schneidet die Gerade P1,1 aus der Geraden P0,E einen weiteren Hilfspunkt 2. Der Schnittpunkt S der Geraden P0,1 mit P2,2 ist dann ein weiterer Punkt des Kegelschnitts k.

Aufgabe: Kegelschnitte über perspektive Kollineation
Aufgabe: Papierstreifenkonstruktion der Ellipse und Stechzirkelkonstruktion der Hyperbel
Aufgabe: Für eine Hyperbel gilt: Schneidet eine beliebige Gerade g die Hyperbel nach zwei Punkten R und S sowie die Asymptoten in den Punkten R1 und S1, so sind die Strecken R1,R und S1,S gleich lang.
Aufgabe: "Fadenkonstruktion" der Parabel: Von einer Parabel sind zwei Punkte Q0 und Q2 samt Tangente bekannt; der Schnittpunkt der beiden Tangenten werde mit Q1 beschriftet. Wird die nun folgende Vorschrift befolgt, so liegt der so konstruierte Punkt Q11 auf der Parabel: Q01 teilt die Strecke Q0,Q1 im Verhältnis k, Q12 teilt die Strecke Q1,Q2 ebenfalls im Verhältnis k und Q11 teilt die Strecke Q01,Q12 im Verhältnis k. Zusätzlich gilt: die Strecke Q01,Q12 ist die Tangente der Parabel im Punkt Q11. (Algorithmus von "DE CASTELJAU")
Aufgabe: Erweitert man die Vorschrift zur Konstruktion eines Punktes in der vorigen auf drei aufeinanderfolgende Strecken Q0,Q1 bzw. Q1,Q2 bzw. Q2,Q3, so erhält man eine Bezierkurve 3.Ordnung, die in vielen CAD-Systemen bzw. Zeichenprogrammen als "allgemeine Kurven" zur Verfügung stehen.