0. Einleitung
1.
Methodische und didaktische Aspekte
2.
Wahlpflichtfächerübergreifende Themenkreise
3.
Projektbeispiele zu den Themenkreisen
4. Bemerkungen
Rahmenbedingungen der Lehrveranstaltung
Der folgende Artikel dokumentiert das, in den Schuljahren 1994/95 und 1995/96 am GRG VIII in Wien durchgeführte Projekt zu obigem Thema. Das im Zuge der Oberstufenreform an der AHS eingeführte Wahlpflichtfachmodell sieht vor, daß Schüler der 5. Klasse AHS/RG aus einem vorgegebenen Fächerkanon insgesamt 10 Stunden in der 6., 7. Und 8.Klasse zu je 2 Wochenstunden buchen. Dabei ist es wichtig, Entscheidungshilfen beim Verplanen der Unterrichtseinheiten anzubieten. Als langjähriger Klassenvorstand am traditionell naturwissenschaftlichen RG in Wien VIII, Albertgasse 18, habe ich die Schüler über die entsprechenden Wahlmöglichkeiten aufgeklärt. Dabei ergaben sich Schülergruppen, die sich unter anderem für die Wahlpflichtfächer Mathematik (vertiefend, Mv), Informatik (zusätzlich, INFz) und Darstellende Geometrie (vertiefend, DGv) entschieden haben. Somit bot die Gelegenheit, eine Klasse einerseits in den Pflichtgegenständen Mathematik und Darstellende Geometrie, andererseits Schülergruppen in den Wahlpflichtgegenständen (WPF) unterrichten zu können, besondere pädagogische und didaktische Möglichkeiten.
Die Lehrveranstaltungen Mv, INFz und DGv waren anfänglich nicht als untereinander vernetzt gedacht. Erst durch organisatorische Basisparameter, wie
1. Methodische und didaktische Aspekte
Eine wesentliche Voraussetzung für die Themenfindung in den Wahlpflichtfächern war eine „Bestandsaufnahme" der dafür nötigen Lehrinhalte der Pflichtgegenstände Mathematik und Darstellende Geometrie. Der jeweilige (zu Kursbeginn vorgestellte) Themenkatalog für die zu vertiefenden Kapitel hatte regulierenden Vorschlagscharakter und war, bedingt durch eine bestimmte Erwartungshaltung seitens der Teilnehmer, nachjustierbar.
Als prinzipielle Unterrichtsform wurde der durch den Lehrer angeleitete, konstruktive Arbeitsunterricht gewählt. Die vernetzte Themenbehandlung wurde in vagen Ansätzen vorbereitet und mit Methoden des wissenschaftlichen Arbeitens vertieft. Besonders großer Wert wurde auf die „Entdeckung" fächerübergreifender Aspekte durch die Schüler gelegt. Praxisorientierte Anwendungen (im Sinne innovativer Nischenlösungen) trugen zur Lebendigkeit des Unterrichtes bei. Auf der Basis dieser methodisch und didaktisch gewachsenen Strukturen konnten inhaltliche Grenzen als Schnittstelle zum universitären Bereich erkannt und fallweise durch Hilfestellungen unterschiedlichster Art überwunden werden.
Die gruppendynamische Analyse der WPF-Projektgruppe kann als harmonisch bezeichnet werden. Die Teilnehmer zeigten stets positive Einzel- und Teamarbeitshaltung. Sie waren interessiert an der Auseinandersetzung mit der Sache und um eine entsprechende Dokumentationsform der Themen sehr bemüht. Diese erfolgte meistens durch Artikel oder Protokolle. Dabei war für die Schüler auch Gelegenheit, sich in der Praxis des wissenschaftlichen Arbeitens zu üben. Als technisches Hilfsmittel besaß jeder Schüler den graphikfähigen Taschenrechner TI-81 von Texas Instruments, der schon im Kernunterricht ab der 6. Klasse zur Verfügung stand. Der Einsatz des Rechners, auch als Visualisierungshilfe, hat sich stets bewährt und wurde als fixer Bestandteil im Arbeitsprozeß betrachtet.
Die Behandlung entsprechender Themenbereiche mittels Computeralgebra-Software (wie z.B. Mathematica) war wegen diesbezüglich mangelhafter Hardwareausstattung der Schule nicht möglich, würde jedoch neue Möglichkeiten eröffnen. So sollte an dieser Stelle überhaupt das Wahlpflichtfach Informatik als „nützliches Werkzeug" zur Behandlung von Problemlösungsstrategien gesehen werden, das sich nur an der zur Verfügung stehenden Hard- und Softwarekonfiguration orientieren kann. Einige Teilnehmer des Wahlpflichtfaches INFz programmierten deshalb einfache Graphik - Modul - Sequenzen in höheren Programmiersprachen, die der Visualisierung mathematischer und geometrischer Inhalte dienten.
Für Darstellende Geometrie wurde das CAD-3D Softwarepaket der TU-Wien (Institut für Geometrie) verwendet, das der Autor dieses Artikels in der Version „DGv V1.0" der Schulhardware angepaßt hat. Am Ende des Schuljahres 1994/95 wurden die Ergebnisse des fächerübergreifenden Arbeitsunterrichtes im Rahmen einer kleinen Ausstellung in der Schule präsentiert und somit der naturwissenschaftliche Bereich des Schulprofils betont.
Die Reflexionen der Schüler über die vernetzte
Lehrveranstaltung waren positiv und durch Zufriedenheit über die geleistete
Arbeit geprägt. Für die WPF - Projektgruppenteilnehmer bedeutete
die Entscheidung für diese Fächer nicht nur, daß sie ihren
Ausbildungsschwerpunkt in der Oberstufe der AHS auf den naturwissenschaftlichen
Sektor gelegt haben, sondern auch die damit verknüpften Prüfungen
im Rahmen der Reifeprüfung 1996.
2. Wahlpflichtfächerübergreifende Themenkreise
In den Schuljahren 1994/95 und 1995/96 wurden folgende fächerübergreifende Themenkreise behandelt
3.
Projektbeispiele zu den Themenkreisen
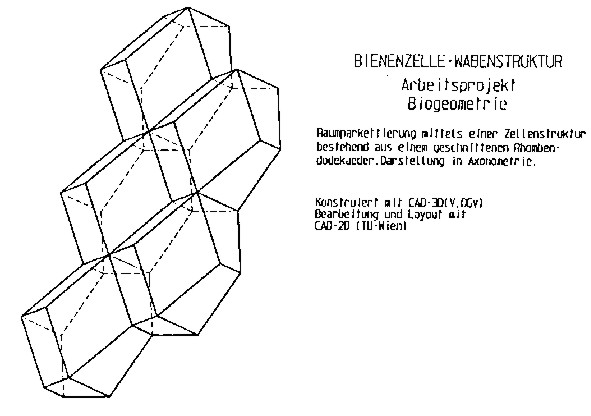
Die Geometrie der Bienenwabenzelle
Der Begriff „Bionik" geht auf die Wortschöpfung „bionics"
des amerikanischen Luftwaffenmajors J.E. Steele zurück. Dieser hatte
im Jahre 1960 eine Tagung einberufen, die sich unter anderem zum Ziel gesetzt
hatte, vom „biologischen Sonar" der Fledermäuse etwas für die
technische Verbesserung des Radars zu lernen. Wir wollen unter „Bionik"
ein Lernen von der Natur als Anregung für eigenständig-technisches
Gestalten verstehen. Bionik als Wissenschaftsdisziplin befaßt sich
systematisch mit der technischen Umsetzung und Anwendung von Konstruktionen,
Verfahren und Entwicklungsprinzipien biologischer Systeme.
| Technische Biologie |
|
Bionik
|
| Technik (vorhandenes Wissen) |
Technik (neue Fragestellungen)
|
- Geometrische Analyse |
Einige Informationen zum Umfeld des Themas:
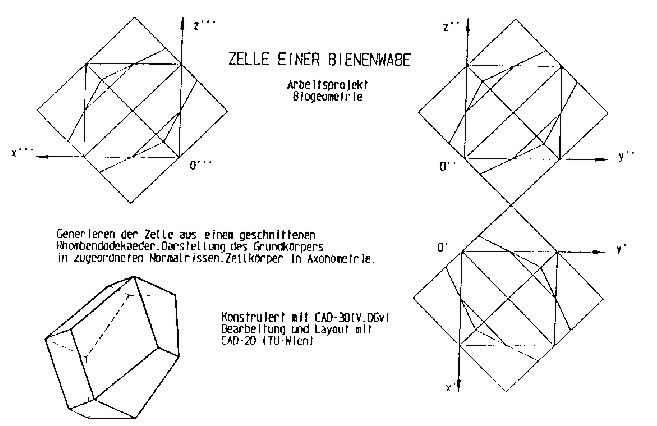
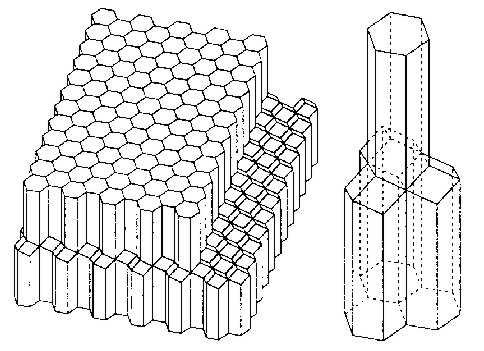
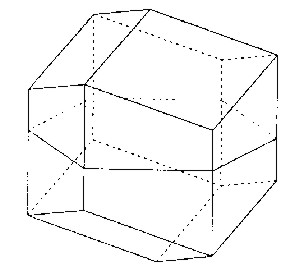
Darstellung einer Bienenwabenzelle in normaler Axonometrie (Aufbauverfahren) als ebener Schnitt eines Rhombendodekaeders.
Ausgangswürfel (a=6cm), Axonometrieangabe: alpha(x)=45°, alpha(y)=15°, vx=2/3 , vy=1 , vz=5/6 ; DIN A4 Querformat , Op[130/100] (gemessen in mm von der linken unteren Blattecke).
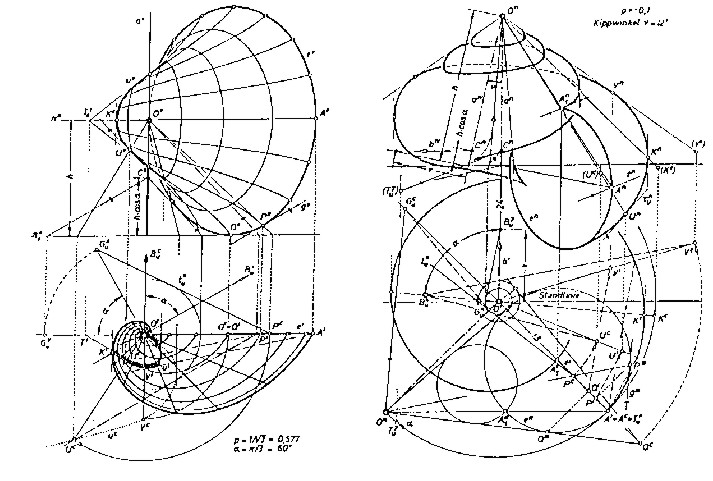
Eine weitere Anregung für biogemetrische Fragestellungen bieten die Abbildungen der Muschelschale und des Schneckengehäuses, die Spiralflächen sind [1].
Weitere geplante Projektthemen:






Analytische Differentialgeometrie von Kurven im R2 und R3
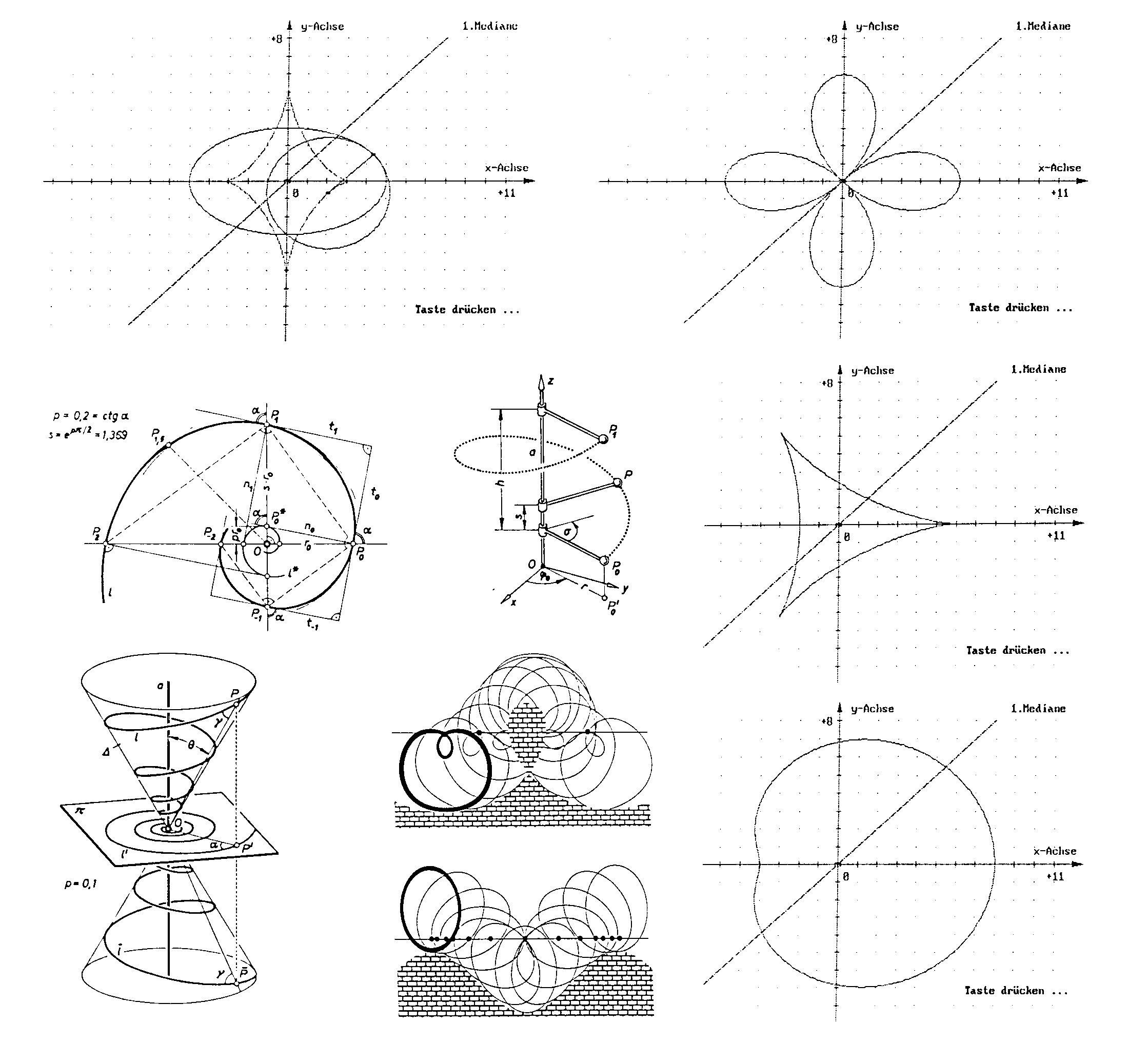
Bei der thematischen Betrachtungsweise wurden die Kurven je nach Bauart in expliziter, impliziter, parametrisierter und in Polarkoordinatendarstellung behandelt. Abgesehen von der elementaren Diskussion des Graphen der Kurve, wurde besonders die Krümmungstheorie berücksichtigt. Die untenstehende Abbildung zeigt die visualisierte Lösung des Krümmungskreises in einem allgemeinen Ellipsenpunkt samt Evolute des Kegelschnitts. Logarithmische Spiralen [2], sowie Schraublinie und räumliche Spiralung, wurden ebenso diskutiert, wie auch die Trochoidenbewegung (als Anwendung der ebenen Kinematik) neben mathematischer Analyse mittels Graphik-Modul visualisiert wurde. Einige weiterführende Überlegungen hatten übrigens durchaus unterhaltsamen Charakter [4] ...
Die Geometrie des Wankel - Motors
Der seinerzeit vieldiskutierte, bei den NSU-Werken nach den Ideen von F. Wankel entwickelte Kreiskolbenmotor ist eine Verbrennungskraftmaschine, die nach dem Viertakt-Ottoprinzip arbeitet. Während aber den üblichen Ottomotoren ein Schubkurbelgetriebe zugrundeliegt, das die hinundhergehende Bewegung des Kolbens im Zylinder mittels der Pleuelstange in eine Drehbewegung umsetzt, beruht der Wankel-Motor auf einer Planetenbewegung:
Ein dreieckiger „Kolben" oder „Läufer" mit gewölbten Seiten rotiert in einem länglichen Gehäuse, dessen Form durch eine gestreckte Epitrochoide der Charakteristik 1:3 festgelegt ist, die von allen drei Kolbenkanten gemeinsam durchlaufen wird. Hierbei bilden sich zwischen Kolben und Gehäusewand drei veränderliche Kammern, in welchen sich der bekannte Viertakt-Prozeß abspielt: Ansaugen des Kraftstoff-Luft-Gemisches durch den Einlaßschlitz, Verdichtung, durch eine Zündkerze ausgelöste Verbrennung (Arbeitstakt), Ausstoßen der Abgase durch den Auslaßschlitz. Bei einer vollen Kolbenumdrehung spielt sich dieser Prozeß in allen vier Kammern ab, und zwar mit einer Phasendifferenz von 120°.
Bestechende Vorteile des Wankel-Motors sind mithin der Wegfall von Ventilen und die Vermeidung von Massenkräften, wie sie das Beschleunigen und Abbremsen oszillierender Teile bedingt. Der Motor besitzt nur zwei bewegliche Teile: den Läufer und die Motorwelle, deren Exzenter im Läufer drehbar gelagert ist. Im Läufer sitzt ein hohler Zahnkranz, der mit einem am Gehäuse befestigten Stirnrad kämmt. Während einer Umdrehung des Läufers erfolgen drei Zündungen und die Motorwelle macht drei Umdrehungen.
Ein schwieriges technisches Problem war die einwandfreie Abdichtung
des Läufers gegen die Gehäusewände. Ein interessantes geometrisches
Problem betrifft die Formgebung des Läufers. Die Ausführung mit
ebenen Seitenflächen würde keine genügende Kompression bedeuten.
Aus diesem Grund werden die Seitenflächen gewölbt, und dabei
erhebt sich die Frage nach dem äußersten zulässigen Maß
der Wölbung, der durch die Zylinderwand Grenzen gesetzt sind. Das
praktisch verwendete Läuferprofil weicht von der theoretischen Grenzform
nur geringfügig ab. Die gewölbten Kolbenwände erhalten übrigens
noch wannenförmige Ausnehmungen, um das richtige Verdichtungsverhältnis
zu erzielen [1].
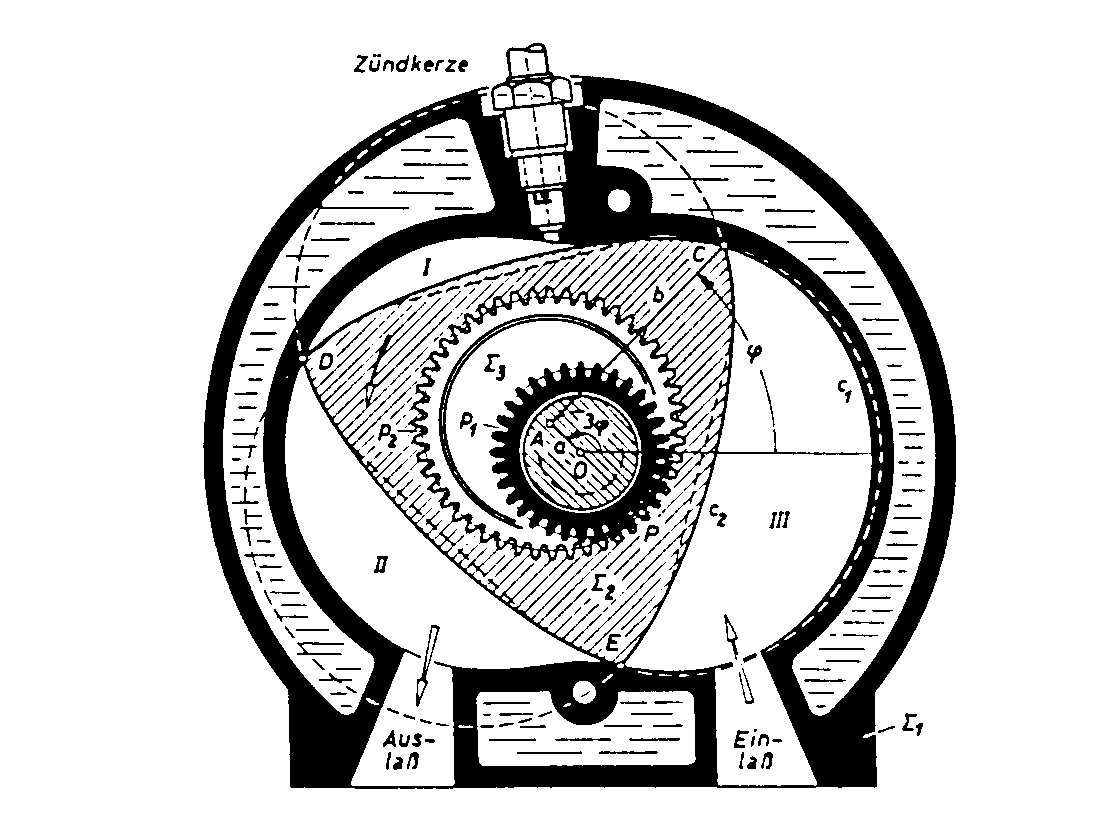
Kreiskolbenmotor von WANKEL
Die Joukowski-Abbildung als Anwendung der Komplexen Zahlen
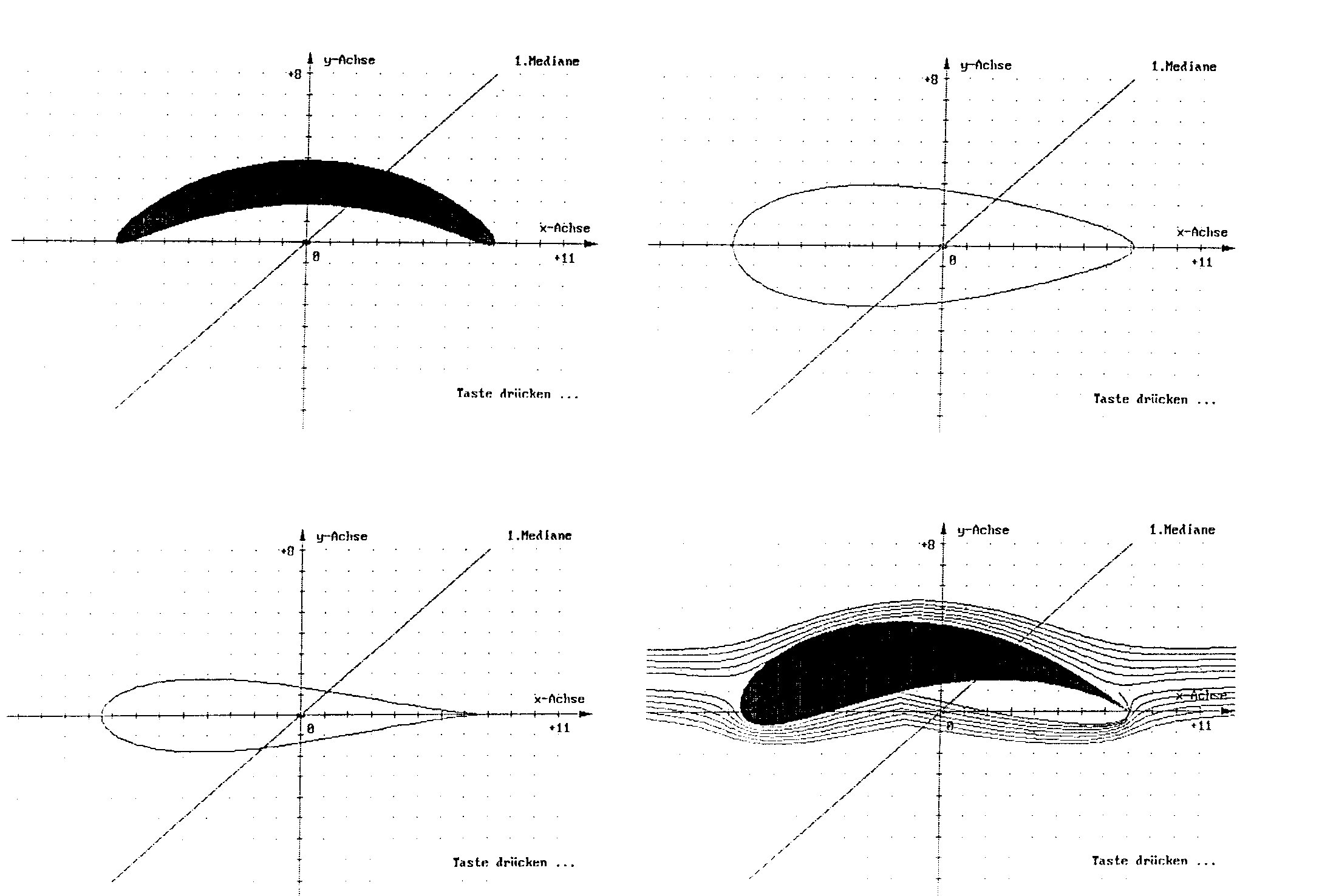
Wenn man bei der Joukowski-Transformation (bei der es sich übrigens um eine konforme Abbildung handelt) in der Darstellung
f(z) = z + c²/z (*)
die komplexe Zahl z = x + iy aufspaltet, läßt sich nach geeigneter Umformung ein brauchbarer Ansatz für eine PC-Visualisierung finden: Spiegelt man nämlich einen Punkt P(x/y) der kartesischen Ebene an einem Kreis in Mittelpunktslage mit dem Radius c, und spiegelt anschließend noch an der x-Achse, so erhält man nach graphischer Anwendung von (*) den transformierten Punkt. Unterwirft man nun sämtliche Punkte der Peripherie des Kreises dem erklärten Verfahren, so erhält man Joukowski-Profile. Ihre Gestalt wird durch die entsprechende Wahl der Parameter bestimmt. Praktische Anwendung findet die Joukowski-Abbildung als „Modellierhilfe" bei der Erstellung von Tragflügelprofilen. Nimmt man bei der Transformation auch noch die mit dem Kreis verknüpften Stromlinien mit, so hat man ein, durch PC-Simulation unterstütztes, einfaches Modul zur Verfügung, das für weitere Arbeitsanregungen dienen kann.
Einführung in die elementare Flächentheorie
Dieses Arbeitsgebiet wurde als eines der aufwendigsten in der WPF-Projektgruppe empfunden:
Das Ergebnis einer sensiblen „Gratwanderung" zwischen Schulgeometrie und universitären Inhalten wird in den nachstehenden Abbildungen deutlich, die ihrerseits Auskoppelungen aus der WPF-Ausstellung und einschlägiger Fachliteratur [3] sind.
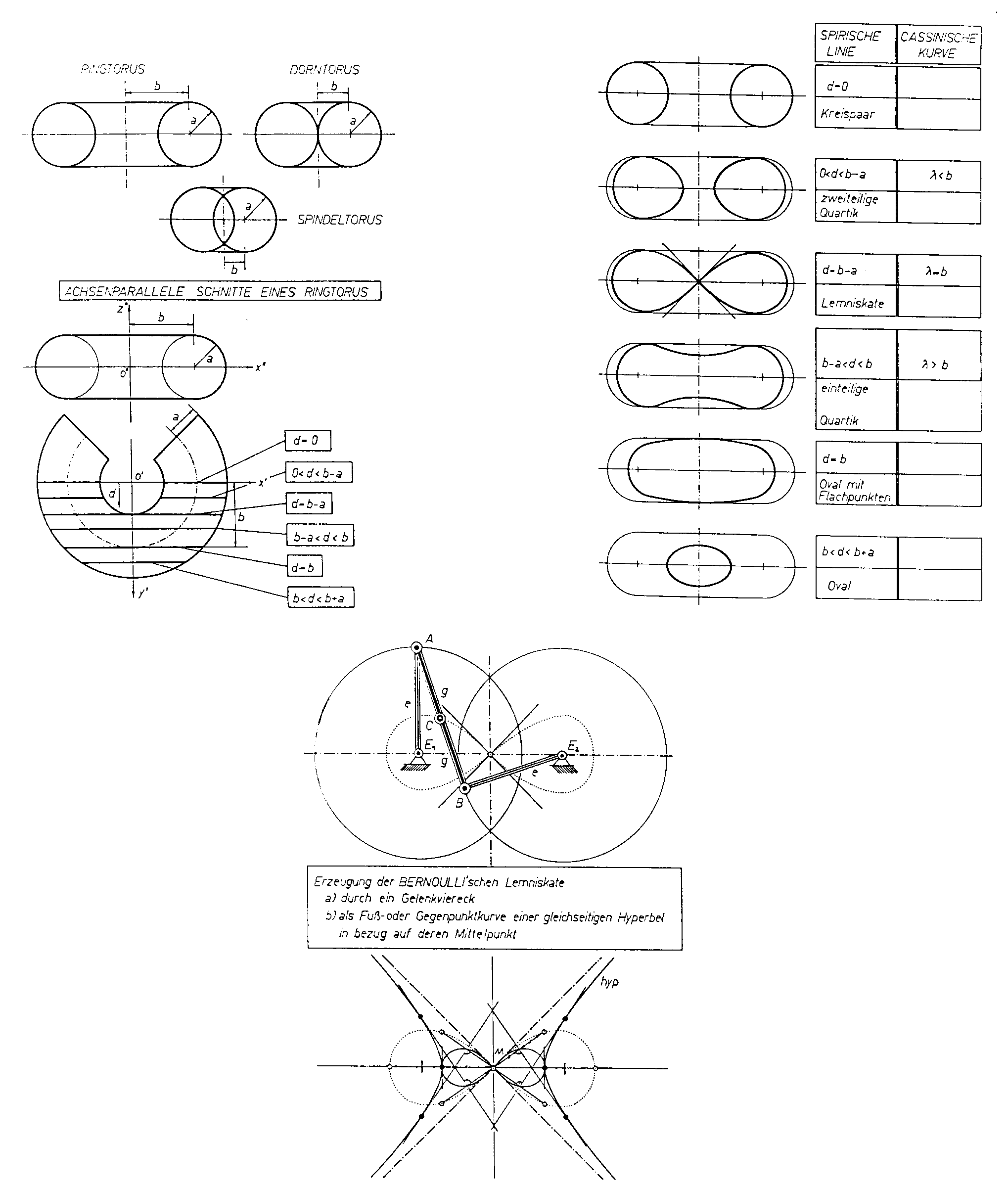
Die Schraubflächen wurden ansatzweise behandelt. Besonders widmete sich die Gruppe den Drehflächen und hier speziell dem Torus. Genau wurden die achsenparallelen Schnitte eines Ringtorus untersucht, wobei man die Bernoulli’sche Lemniskate dabei einer umfassenden Diskussion unterzog.
Das Viviani’sche Fenster, (es ergibt sich im Schnitt einer Kugel mit einem Zylinder, wobei der Kugelradius gleich dem Zylinderdurchmesser ist) als Beispiel für die Durchdringung zweier „in Berührung" befindlicher Flächen, sorgte durch die Eigenschaft, daß die Raumkurve geometrischer Ort von gleicher geographischer Länge und Breite auf der Kugel ist, für Erstaunen.
Kotierte Projektion (Aufgaben aus dem Straßenbau)
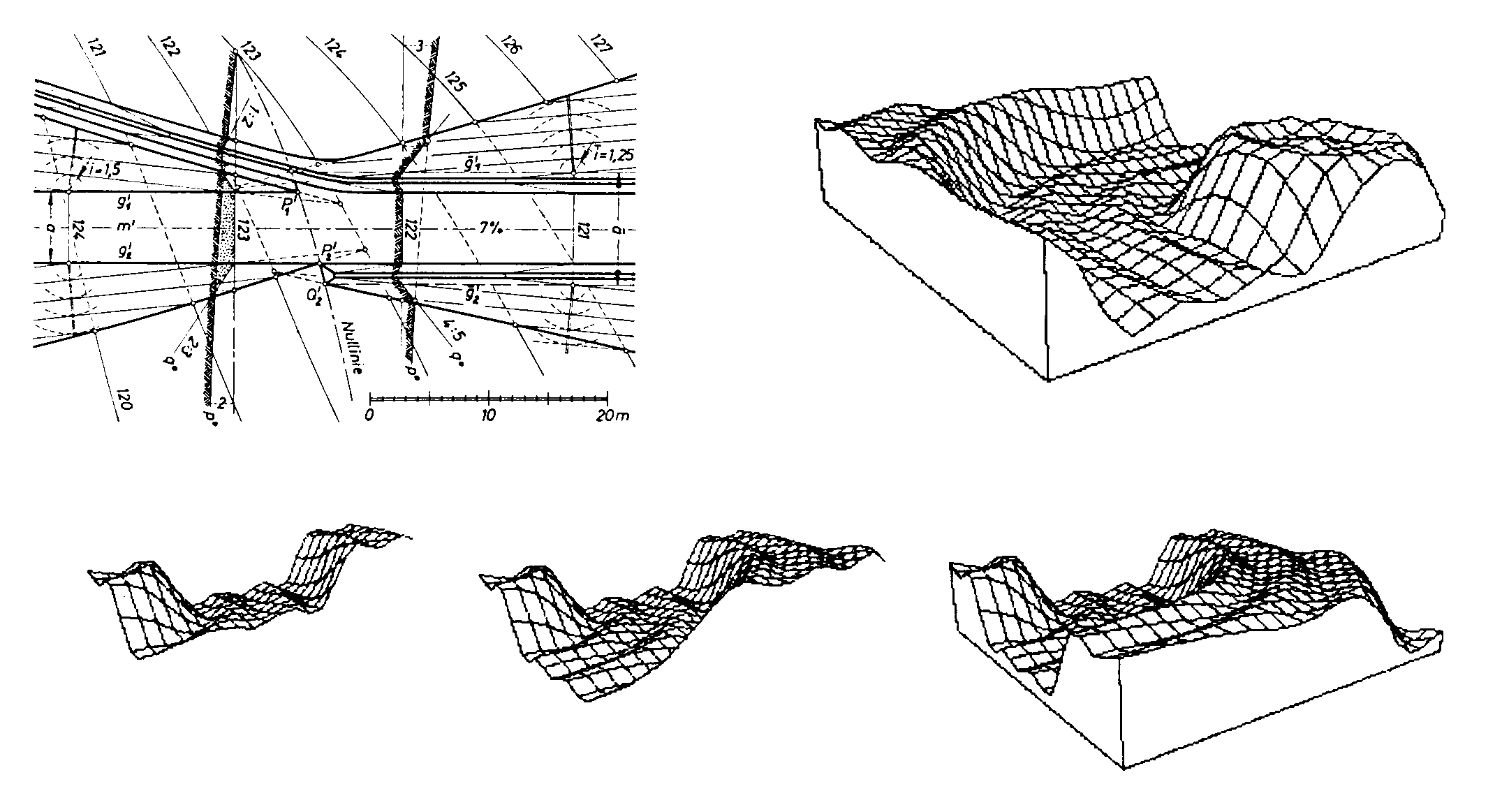
In ein zunächst theoretisch eben geböschtes Gelände wurde eine Straße mit den nötigen Dämmen und Einschnitten projektiert. Beim Übergang der geraden Straßenmittellinie in eine kreisförmige wurde ein Klothoidenbogen verwendet. Dabei bot sich erneut Gelegenheit, das Krümmungsverhalten von Kurven zu studieren. Mit einem Ausblick auf natürliche Geländeflächen und ihre approximative Erfassung als numerisches Problem wurde das Thema abgerundet.
Die nachstehende Abbildung zeigt eine, in ein natürliches Gelände projektierte, geradlinig verlaufende, ansteigende Straße mit den nötigen Dämmen, Einschnitten und Wassergräben [8]. Die Vermaschung eines Geländes mit Hilfe mathematischer, parametrisierter Flächen eröffnet die Möglichkeit für einen fraktalen Geländeansatz, der hier in einer visualisierten Metamorphose zu sehen ist.
Die Arbeitsprozesse und ihre Ergebnisse erfolgten ohne
den traditionellen „Schuldruck", was natürlich von der Schülergruppe
abhängig war. Für das positive Gelingen eines derartigen Projektes
muß die Bereitschaft dazu vorhanden sein, weil der entsprechende
Arbeitsaufwand in der Vorbereitungs-, Durchführungs- und Nachbereitungsphase
beachtlich ist. Große Flexibilität ist jedenfalls bei der konkreten
Umsetzung der vorbereiteten Arbeitssequenzen angebracht. Damit bietet der
wahlpflichtfächerübergreifende Unterricht die Chance, die sich
ergebenden Freiräume für neue pädagogische Qualitäten
zu nützen.
[1] W. Wunderlich; Ebene Kinematik, BI-HTB, 1968.
[2] W. Wunderlich: Darstellende Geometrie II, BI-HTB, 1967
[3] Giering, Seybold; Konstruktive Ingenieurgeometrie, Hanser-Verlag, 1987
[4] Spektrum der Wissenschaft, 3/1994
*********************************
Für weitere Informationen stehe ich gerne zur Verfügung:
Mag. Alfred KOUTENSKY, GRG VIII, Albertgasse 18-22, 1080 Wien
Tel.: 405 61 15 /15 Fax : 405 61 15 / 55