|
Chain Geometry
The aim of the project is to investigate various aspects of the generalised chain geometry arising from the projective line over a ring which contains a (possibly skew) field.
|
|
|
Chain Geometry over Skew Fields
|
|

|
Principal Investigator: Andrea Blunck
Austrian Science Fund (FWF) Lise Meitner fellowships M529-MAT and M574-MAT
Austrian Co-Applicant: Hans Havlicek
|
|
|
What is a Chain Geometry?
Let R be a ring with unity and let F be a field contained in R as a subring. The chain geometry Σ(F,R) is an incidence structure with point set ℙ(R), i. e. the projective line over R. The projective line over F can be considered as a subset of ℙ(R). Its images under the group of projectivities are the chains.
|
 Stereographic projection
Miquel's theorem
|
The Classical Example
Here R is the field ℂ of complex numbers and F is the field ℝ of reals. The corresponding chain geometry is an algebraic model for the Euclidean Möbius plane, i.e., the Euclidean plane with one extra "point at infinity". The ℝ-chains correspond exactly to the circles and lines of the plane (with the extra assignment that all lines contain the point at infinity). The term chain goes back to Karl G. C. von Staudt (1798-1867).
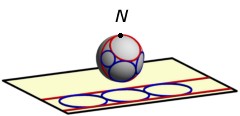
Another model for the projective line ℙ(ℂ) is a sphere in Euclidean 3-space; the ℝ-chains appear exactly as the circles on the sphere.
The link between these two geometric models is the stereographic projection from the "north pole" N: Each point of the sphere (other than N) is projected to a plane which is parallel to the plane of the "equator". The point N, however, is mapped to the point at infinity.
The second picture on the left hand side illustrates a theorem due to A. Miquel (published 1838) in the Euclidean Möbius plane. The underlying configuration consists of 8 points and 6 circles such that there are
- 4 points on each circle
- 3 circles through each point.
This theorem holds - mutatis mutandis - in many other chain geometries.
|
 Distant graphs of projective lines
|
Distant Graph
A basic notion for the projective line ℙ(R) over a ring R is the relation distant. Non-distant points are also called parallel. This terminology goes back to the projective line over the real dual numbers, where parallel points represent parallel spears of the Euclidean plane (cf. below).
The points of ℙ(R) are the vertices and the unordered pairs of distant points are the edges of the distant graph.
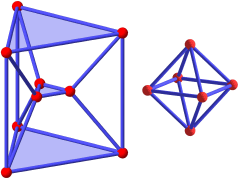
For example, if GF(2) is the field of integers modulo 2 then the projective line over GF(2) × GF(2), i. e the ring of double numbers over GF(2), has a distant graph which is depicted on the very left. It has 9 vertices, the shaded triangles serve only for better visualisation.
If R is the ring of integers modulo 4 or the ring of dual numbers over GF(2), then the distant graph of ℙ(R) is isomorphic to a regular octahedron. So, non-isomorphic rings may have isomorphic distant graphs.
One of our main results is as follows: The distant graph of a projective line ℙ(R) is connected if, and only if, the underlying ring R is a GE2-ring. This means that the group GL2(R) of invertible 2x2-matrices over R is generated by the set of all elementary and invertible diagonal matrices.
|
Stereographic projection of Blaschke's cylinder
|
Another Famous Model: Blaschke's Cylinder
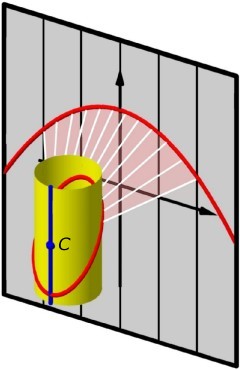
By a result due to Wilhelm Blaschke, the projective line over the ring R = ℝ[ε], ε2=0, of real dual numbers can be represented as a cylinder in affine 3-space. The ℝ-chains of ℙ(ℝ[ε]) correspond with the non-degenerate conics on this cylinder. Two points of the cylinder are non-distant (parallel) if, and only if, they are on a common generator.
Up to isomorphism the chain geometry based on (F,R) = (ℝ,ℝ[ε]) coincides with the Euclidean Laguerre geometry (spears and oriented circles of the Euclidean plane) and the 3-dimensional space-time geometry with signature (2,1).
Let us consider the stereographic projection of Blaschke's cylinder (see the picture on the left). All but one generators of the cylinder are mapped to a pencil of parallel lines. They turn the image plane into an isotropic plane. The exceptional blue generator contains the centre C of projection and it is mapped onto a generator at infinity which has to be added to the affine isotropic plane. (This is not the projective closure of an affine plane!)
The images of the conics on the cylinder fall into two classes: A conic that does not pass through C goes over to a parabola with isotropic diameters. A conic that runs through the centre C is mapped onto a non-isotropic line.
So the chain geometry based on (ℝ,ℝ[ε]) is also an algebraic model for the isotropic plane with one extra generator at infinity.
|
|
|
Projective Models
The link between the projective line ℙ(R) over a ring R and classical projective geometry is given by a projective model. Here the points of ℙ(R) appear as certain subspaces of a projective space over a field F. Algebraically, such a model is based upon an injective homomorphism of R into the endomorphism ring of an F-vector space.
We present some low dimensional examples:
|

Regulus with two transversal lines
|
Matrix Rings. The projective line over the ring R of 2 by 2 matrices over a field F (viz. R = F2x2) is represented by the set of all lines of a 3-dimensional projective space over F.
If F is embedded into R via scalar matrices diag(x,x), then each F-chain appears as a regulus and, conversely, each regulus arises in this way. Here a regulus is the set of all lines that meet three mutually skew lines (called transversals).
The picture on the left hand side shows a regulus in the real projective space (F=ℝ) together with two of its transversals. (In our image the regulus is one family of generators of a hyperbolic paraboloid.)
Similar results hold if R is the endomorphism ring of an arbitrary vector space over F, but the definition of a regulus is more sophisticated, especially in the infinite dimensional case.
|
 Elliptic linear congruence (regular spread)
|
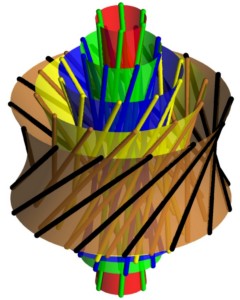
Complex Numbers. As has been sketched above, the projective line over ℝ2x2 corresponds to the set of all lines of the real projective 3-space. If the complex numbers ℂ are embedded in ℝ2x2 in the usual way, then each ℂ-chain appears as elliptic linear congruences of lines (regular spread) and, conversely, each elliptic congruence arises in this way.
The picture shows one such congruence of lines. It has the remarkable property to send precisely one of its lines through each point of the space. For better visualisation we have partitioned the congruence into reguli that belong to the quadrics of a pencil of hyperboloids of revolution; also the common axis of revolution (not drawn!) and the line at infinity of the horizontal planes (not drawn either!) belongs to the congruence.
If we choose just one elliptic congruence of lines then it is a model of the complex projective line ℙ(ℂ).
The ℝ-sublines of ℙ(ℂ) appear as the reguli contained in the congruence. You can see some of those reguli on our picture.
In the Euclidean Möbius plane those reguli correspond to a pencil of concentric circles, the two extra lines represent their common midpoint and the point at infinity.
These results remain true (with some minor modifications) if an arbitrary quadratic field extension L/F is taken instead of ℂ/ℝ.
|
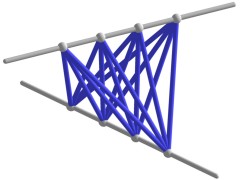
Hyperbolic linear congruence
|
Double Numbers. Another example that admits an easy visualisation is the ring F × F of double numbers over a field F.
A projective model is given by a hyperbolic linear congruence of lines in a projective 3-space over F, i.e., the set of all lines that meet two skew axes.
As above, the F-chains appear as the reguli contained in the congruence. Here F is embedded in F × F by identifying each element x of F with the pair (x,x).
Similar results hold for the ring Fn: A projective model in a (2n-1)-dimensional projective space is given by all (n-1)-dimensional subspaces that meet n lines in general position.
|

Parabolic linear congruence
|
Dual Numbers. The projective line over the ring F[ε], ε2=0, of dual numbers over a field F can be represented by a subset of a parabolic linear congruence of lines. Such a congruence has just one axis which belongs to the congruence. The axis is the only line of the congruence that represents no point of the dual projective line. As in the hyperbolic case, all lines of the congruence through a point on the axis form a pencil. The mapping that assigns to each point P of the axis the carrier plane of the pencil with centre P is a projectivity.
The F-chains appear exactly as the reguli contained in the congruence.
|

Special linear complex
|
Ternions. The ring of ternions over a field F is isomorphic to the ring of upper triangular 2x2 matrices over F. The projective line over this ring is represented by lines of a special linear complex, i.e., the set of all lines in a 3-dimensional projective space that meet a fixed axis; only this axis represents no point of the projective line over the ternions.
The F-chains appear as the reguli that have the axis of the complex among their transversal lines.
|
|
|
Publications
-
H. Havlicek: Eine affine Beschreibung von Ketten, Abh. Math. Sem. Univ. Hamburg 53 (1983), 267-276.
-
H. Havlicek: Die Projektivitäten und Antiprojektivitäten der
Quaternionengeraden, Publ. Math. Debrecen 40 (1992), 219-227.
Preprint (PDF)
-
H. Havlicek: On the geometry of field extensions, Aequat. math. 45 (1993) 232-238.
Preprint (PDF)
-
H. Havlicek: Spreads of right quadratic skew field extensions, Geom. Dedicata 49 (1994), 239-251.
Preprint (PDF)
-
H. Havlicek: Spheres of quadratic field extensions, Abh. math. Sem. Univ. Hamburg 64 (1994), 279-292.
Preprint (PDF)
-
A. Blunck: A Quadric Model for Klingenberg Chain Spaces, Geom. Dedicata 55 (1995), 237-246.
-
A. Blunck and M. Stroppel: Klingenberg Chain Spaces, Abh. Math. Sem. Univ. Hamburg 65 (1995), 225-238.
-
H. Havlicek: Invariant points of circular transformations, RAD Hrvatske akademije znanosti e umjetnosti 470, Knjiga XLVI, Matematicke znanosti 12 (1995), 113-118.
Preprint (PDF)
-
A. Blunck: Generalized Affine Chain Geometries, J. Geometry 56 (1996), 9-17.
-
A. Blunck: Chain Spaces via Clifford Algebras, Monatsh. Math.123
(1997), 93-107.
-
H. Havlicek: Affine circle geometry over quaternion skew fields, Discrete Math. 174 (1997), 153-165.
Preprint (PDF)
-
A. Blunck: Geometries for Certain Linear Groups over Rings - Construction
and Coordinatization, Inaugural Thesis, Darmstadt University of Technology,
1997.
-
A. Blunck: Regular spreads and chain geometries, Bull. Belg. Math. Soc. Simon Stevin 6 (1999), 589-603.
-
A. Blunck, H. Havlicek: Affine spaces within projective spaces, Result. Math. 36 (1999), 237-251.
Preprint (PDF)
-
A. Blunck: Reguli and chains over skew fields, Beiträge Algebra Geometrie 41 (2000), 7-21.
-
A. Blunck, H. Havlicek: Extending the concept of chain geometry, Geom. Dedicata 83 (2000), 119-130.
Preprint (PDF)
-
A. Blunck, H. Havlicek: Projective representations I: Projective lines over a ring, Abh. Math. Sem. Univ. Hamburg 70 (2000), 287-299.
Preprint (PDF)
-
A. Blunck, H. Havlicek: Projective representations II: Generalized chain geometries, Abh. Math. Sem. Univ. Hamburg, 70 (2000), 301-313.
Preprint (PDF)
-
A. Blunck, H. Havlicek: The connected components of the projective line over a ring, Adv. Geom. 1 (2001), 107-117.
Preprint (PDF)
-
A. Blunck: Der Distanzgraph der projektiven Geraden über einem Ring, in S. Handrock, W. Lang (eds.), Tagungsband der 4. Tagung der deutschen Sektion der Europäischen Mathematikerinnen Vereinigung (EWM),
Technische Universität Chemnitz, Chemnitz 2001 (ISBN 300-0076-76-X), pp. 51-53.
-
A. Blunck: Chain spaces with many reflections, J. Geometry 72 (2001), 18-26.
-
A. Blunck: Finite circle planes, in R. Camina, L. Fajstrup (eds.), Proceedings of the Ninth International Conference of European Women in Mathematics, Hindawi, Stony Brook 2001 (ISBN: 977-5945-02-X), pp. 171-176.
-
A. Blunck, H. Havlicek: The dual of a chain geometry, J. Geometry 72 (2001), 27-36.
Preprint (PDF)
-
A. Blunck: Projective groups over rings, J. Algebra 249 (2002), 266-290.
-
A. Blunck, H. Havlicek: Jordan homomorphisms and harmonic mappings, Monatsh. Math. 139 (2003), 111-127.
Preprint (PDF)
-
A. Blunck, H. Havlicek: Radical parallelism on projective lines and non-linear models of affine spaces, Math. Pannon. 14 (2003), 113-127.
Preprint (PDF)
-
H. Havlicek, K. List: A three-dimensional Laguerre geometry and its visualization, in: G. Weiß (ed.): Proceedings - Dresden Symposium Geometry: Constructive and Kinematic" (DSG.CK), Institut für Geometrie, TU Dresden, Dresden, 2003, pp. 122-129. (ISBN 3-86005-394-9)
Preprint (PDF)
-
A. Blunck, H. Havlicek: On distant-isomorphisms of projective lines, Aequationes Math. 69 (2005), 146-163.
Preprint (PDF)
-
H. Havlicek: Divisible Designs, Laguerre Geometry, and Beyond, Summer School on Combinatorial Geometry and Optimisation 2004 "Giuseppe Tallini", Brescia, Italy, July 4th-10th, 2004, 63 pp.
Preprint (PDF)
-
S. Giese, H. Havlicek, and R.-H. Schulz:
Some constructions of divisible designs from Laguerre geometries, Discrete Math. 301 (2005), 74-82.
Preprint (PDF)
-
A. Blunck, H. Havlicek, and C. Zanella: Divisible designs from twisted dual numbers, Des. Codes Cryptogr. 47 (2008), 11-20.
Preprint (PDF)
-
A. Blunck, H. Havlicek, and C. Zanella: Blocking sets in chain geometries, In: F. Mazzocca, N. Melone and D. Olanda (eds.): Trends in Incidence and Galois Geometries. A Tribute to Giuseppe Tallini, Quad. Mat. 19, Aracne Editrice, Roma, 2010, pp. 39-49. (ISBN-13: 978-88-548-3571-9)
Preprint (PDF)
-
H. Havlicek: From pentacyclic coordinates to chain geometries, and back, Mitt. Math. Ges. Hamburg 26 (2007), 75-94.
Preprint (PDF)
-
A. Blunck and H. Havlicek: Projective lines over Jordan systems and geometry of Hermitian matrices, Linear Algebra Appl. 433 (2010), 672-680.
Preprint (PDF)
|
|
Quick Links
Andrea Blunck
Hans Havlicek
Klaus List
Design Theory
Geometry and Quantum Theory
Line Geometry
Spreads and Parallelisms
Sitemap
External Links
Ralph-Hardo Schulz, Free University of Berlin
Corrado Zanella, University of Padua

Austrian Science Fund (FWF)

A. Blunck and A. Herzer,
Kettengeometrien,
Eine Einführung.
Shaker, Aachen, 2005.
This book begins by presenting the basic concepts of Chain Geometry and leads the reader to the most recent developments in this branch of geometry.
Poster
 Geometrie über Ringen
Geometrie über Ringen
(PDF - in German)
|




 Geometrie über Ringen
Geometrie über Ringen