
Abstract:
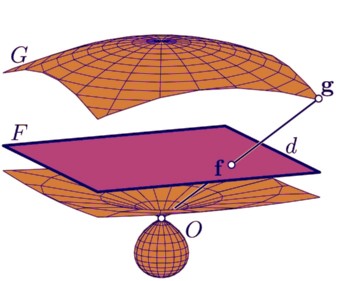
The conchoid surface G of a given surface F with respect to a point O is roughly speaking the surface obtained by increasing the radius function of F with respect to O by a constant d. This paper studies real rational ruled surfaces in this context and proves that their conchoid surfaces possess real rational parameterizations, independently on the position of O. Thus any rational ruled surface F admits a rational radius function r(u, v) with respect to any point in space. Besides the general skew ruled surfaces and examples of low algebraic degree we study ruled surfaces generated by rational motions.Bibtex:
@article{peternell-cs-2011,
author = "Martin Peternell and David Gruber and Juana Sendra",
title = "Conchoid surfaces of rational ruled surfaces",
journal = "Computer Aided Geometric Design",
volume =28,
pages = "427-435",
doi = "http://dx.doi.org/10.1016/j.cagd.2011.07.005",
url = "http://dmg.tuwien.ac.at/dgruber/paper/paper_conch_ruled_surf.pdf",