
Abstract:
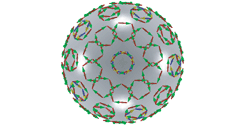
We present two subdivision schemes for the fair discretization of the spherical motion group. The first one is based on the subdivision of the 600-cell according to the tetrahedral/octahedral subdivision scheme of Schaefer, Hakenberg and Warren [Smooth Subdivision of Tetrahedral Meshes. Eurographics Symposium on Geometry Processing (R. Scopigno, D. Zorin, eds.), 151-158, 2004]. The second presented subdivision scheme is based on the spherical kinematic mapping. In the first step we discretize an elliptic linear congruence by the icosahedral discretization of the unit sphere. Then the resulting lines of the elliptic three-space are discretized such that the difference between the maximal and minimal elliptic distance between neighboring grid points becomes minimal.
Bibtex:
@article{nawratil-2008-fdsmg,
author = "Georg Nawratil and Helmut Pottmann",
title = "Subdivision Schemes for the fair Discretization of the Spherical Motion Group",
journal = {J. Comput. Appl. Math.},
year = 2008,
volume = 222,
number = 2,
pages = "574-591",
url="http://dmg.tuwien.ac.at/geom/ig/sn/2008/np_motion_07/np_motion_07.html",
}
|
|