We study redundant ![]() -ary digit expansions
-ary digit expansions
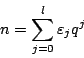
We give an algorithm to compute the ![]() th digit of this ``symmetric
signed digit expansion'' from the knowledge of the
th digit of this ``symmetric
signed digit expansion'' from the knowledge of the ![]() first digits
of the ``standard''
first digits
of the ``standard'' ![]() -ary expansion, i. e., the unique expansion
with digits
-ary expansion, i. e., the unique expansion
with digits ![]() , ...,
, ..., ![]() .
.
Additionally, we give an explicit formula for the ![]() th digit of a
minimal expansion without having to calculate the other digits. This
enables us to calculate the number of occurrences of a given sub-block
among the expansions of the integers up to some
th digit of a
minimal expansion without having to calculate the other digits. This
enables us to calculate the number of occurrences of a given sub-block
among the expansions of the integers up to some ![]() asymptotically.
asymptotically.
We study the average number of carry propagations in von Neumann's addition method. Contrary to the standard case investigated by Knuth, there are positive and negative carries, which makes the situation more delicate.
Finally we deal with the question whether such results can be generalized to other number systems, for instance canonical number systems in an algebraic number field or number systems defined by recurring sequences.