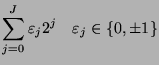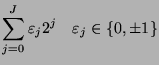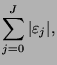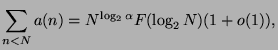Redundant binary representations of integers have been used in cryptography to
speed up computations in Diffie-Hellman encryption schemes. Especially, in the
case of elliptic curve cryptography, where addition and substraction are
equally costly operations, representations of the form
are used. The redundance in the digit set is used to minimize the weight
which represents the number of additions. This has been used by F. Morain and
J. Olivos, who used the special case of the ``non-adjecent form'' (
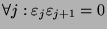 ). We study the number
). We study the number 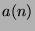 of representations of
minimal weight. This turns out to be related to a measure
of representations of
minimal weight. This turns out to be related to a measure 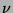 on the interval
on the interval
![$ [-1,1]$](Grabner-img6.png) , which has some similarities to the Erdos measures. We use a
variant of the Jessen-Wintner theorem to show that this measure is singular
continuous. Furthermore, this measure is used to show the asymptotic formula
, which has some similarities to the Erdos measures. We use a
variant of the Jessen-Wintner theorem to show that this measure is singular
continuous. Furthermore, this measure is used to show the asymptotic formula
where 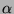 is the largest root of the polynomial
is the largest root of the polynomial
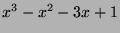 and
and 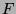 is
a continuous periodic function.
is
a continuous periodic function.
Back to the Index
Please send comments and corrections to Thomas Klausner.