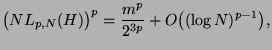We study the 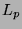 -discrepancy of the digitally shifted Hammersley point set in base 2. It has been shown by
Pillichshammer that for any natural number
-discrepancy of the digitally shifted Hammersley point set in base 2. It has been shown by
Pillichshammer that for any natural number 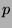 the
the 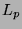 -discrepancy of the unshifted Hammersley point set
-discrepancy of the unshifted Hammersley point set 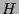 with
with  points satisfies
points satisfies
i. e., the 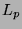 -discrepancy of the unshifted Hammersley point set is of order
-discrepancy of the unshifted Hammersley point set is of order 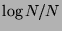 . Here we show that,
for even integers
. Here we show that,
for even integers 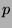 , there always exists a digital shift of the Hammersley point set such that its
, there always exists a digital shift of the Hammersley point set such that its
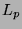 -discrepancy is of order
-discrepancy is of order
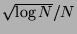 , which is best possible by a result of Schmidt.
For the special case
, which is best possible by a result of Schmidt.
For the special case 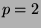 , we give very tight lower and upper bounds on the
, we give very tight lower and upper bounds on the 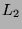 -discrepancy of digitally
shifted Hammersley point sets. These bounds show that the value of the
-discrepancy of digitally
shifted Hammersley point sets. These bounds show that the value of the 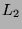 -discrepancy mostly depends on the
number of zeros in the shift vector and not so much on the position of these. We compare our results to an
existing result by Halton and Zaremba and draw some interesting consequences.
-discrepancy mostly depends on the
number of zeros in the shift vector and not so much on the position of these. We compare our results to an
existing result by Halton and Zaremba and draw some interesting consequences.
Back to the Index
Please send comments and corrections to Thomas Klausner.
![]() -discrepancy of the digitally shifted Hammersley point set in base 2. It has been shown by
Pillichshammer that for any natural number
-discrepancy of the digitally shifted Hammersley point set in base 2. It has been shown by
Pillichshammer that for any natural number ![]() the
the ![]() -discrepancy of the unshifted Hammersley point set
-discrepancy of the unshifted Hammersley point set ![]() with
with ![]() points satisfies
points satisfies