Nonlinear congruential pseudorandom number generators have been studied extensively in the
last decades because of the well known deficiencies of the classical linear congruential generators.
It is shown that the sequences generated by nonlinear methods have favourable behaviour.
In this talk we shall report on some recent results on the properties of pseudorandom number generators
defined by a recurrence relation
of order 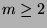 ,
,
Here initial values
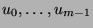 are in the finite field
are in the finite field
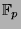 with prime
with prime 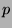 and
and 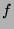 is a rational function in
is a rational function in 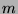 variables over
variables over
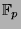 .
Nonlinear generators of
higher
order
.
Nonlinear generators of
higher
order 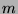 are of particular interest
as the period length of generated sequences can go up to
are of particular interest
as the period length of generated sequences can go up to 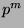 .
.
- 1
-
Jaime Gutierrez, Igor E. Shparlinski, and Arne Winterhof.
On the linear and nonlinear complexity profile of nonlinear
pseudorandom number-generators.
IEEE Trans. Inform. Theory, 49(1):60-64, 2003.
- 2
-
Harald Niederreiter and Igor E. Shparlinski.
On the distribution and lattice structure of nonlinear congruential
pseudorandom numbers.
Finite Fields Appl., 5(3):246-253, 1999.
- 3
-
Alev Topuzoglu and Arne Winterhof.
On the linear complexity profile of nonlinear congruential generators
of higher orders.
(submitted).
Back to the Index
Please send comments and corrections to Thomas Klausner.
![]() ,
,