Kegelschnitte als Ortslinien II - Leitkreiserzeugung

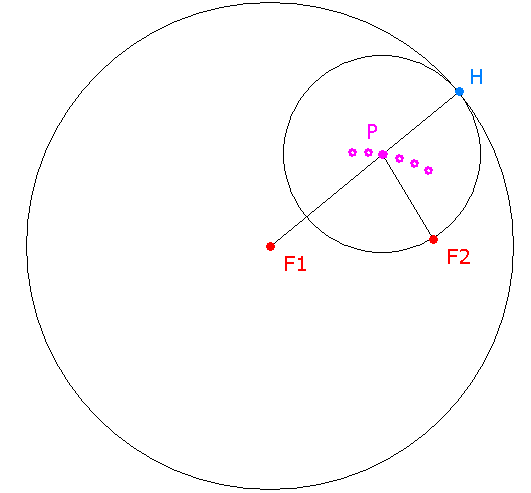
Aufgabe: Gegeben ist ein fester Kreis k mit dem Mittelpunkt F1 und dem Radius 2a. Konstruiere Kreise, die den festen Kreis berühren und die durch einen weiteren festen Punkt F2 verlaufen. Untersuche anschließend die Bahn der Mittelpunkte P dieser Kreise.

Beantworte folgende Fragen:

1. Welche Kurve beschreibt der Mittelpunkt P des variablen Kreises, wenn der Punkt F1 innerhalb des festen Kreises k liegt?
2. Welche Kurve durchläuft P, wenn F1 außerhalb von k liegt?
3. Was passiert, wenn F1 auf dem Kreis k liegt?
4. Erkläre den Sonderfall, dass F1 mit dem Mittelpunkt F2 des festen Kreises zusammenfällt!

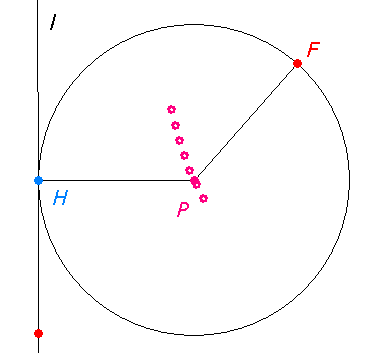
Aufgabe - Sonderfall: Wir ersetzen nun den festen Kreis k durch eine Gerade l und ermitteln wiederum jene Kreise, die die Gerade berühren und die durch einen weiteren festen Punkt F verlaufen. Untersuche ebenfalls die Bahn der Mittelpunkte P dieser Kreise.

Beantworte folgende Fragen:

1. Welche Kurve beschreibt nun der Mittelpunkt P des variablen Kreises?
2. Beobachte die (zur Konstruktion der variablen Kreise notwendige) Streckensymmetrale der Punkte H und F. In welcher "Beziehung" steht diese zur Bahnkurve des Punktes P.
3. Gilt die Eigenschaft (aus Punkt 2) auch in den weiter oben erklärten Fällen?

Lösung und Beweis:

Lösungen:

1. Ellipse
2. Hyperbel
3. Die beiden Kreise fallen zusammen; als Ortslinie entsteht nur der Punkt F1
4. Kreis

1. Parabel
2. Streckensymmetrale ist Tangente an Parabel im Punkt P
3. ja

Bemerkung: Diese Eigenschaft kann (und wird zum Teil auch) zur Tangentenkonstruktion herangezogen werden.

Beweis:

Aus der Figur erkennt man leicht, dass P,F1 + P,F2 = P,F1 + P,H = F1,H = 2a konstant ist.

Bemerkung: Die erste Aufgabe kann auch als Verallgemeinerung der "klassischen" Parabelkonstruktion aufgefasst werden, wenn man in der Definition der Parabel die Leitgerade durch einen Kreis ersetzt.