Offset eines Ellipsoids
Vorwissen
Für die folgende Übung sind folgende Vorkenntnisse empfehlenswert:
- Parameterdarstellung von Flächen
- partielle Ableitungen
- Kreuzprodukt von Vektoren
- Einheitsvektoren (normierte Vektoren)
Ziele
In dieser Übung erarbeiten wir das Offset (Parallelfläche) eines Ellipsoids.
Wiederholung Polarkoordinaten:
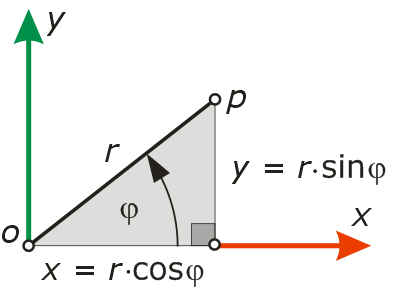Die Figur links erklärt die Umrechnung von Polarkoordinaten in kartesische Koordinaten:
In Verallgemeinerung der ebenen Polarkoordinaten erhalten wir räumliche Kugelkoordinaten wie folgt:
Mehrfachauswahl
Offset eines Ellipsoids
Zur Berechnung des Offsets eines Ellipsoids verwenden wir die folgende Parameterdarstellung
und berechnen die partiellen Ableitungen.
Anmerkung: diese Darstellung entsteht aus der Parameterdarstellung einer Kugel durch Skalierung mit den Faktoren a/r, b/r, c/r.
Welche der folgenden Antworten ist richtig?
| |
| |
| |
| |
| |
| |
Lücken-Aktivität
Verwende zum Ausfüllen des Lückentexts zwei der folgenden Wörter:
parallel, windschief, normal, Kreuzprodukts, skalaren Produkts
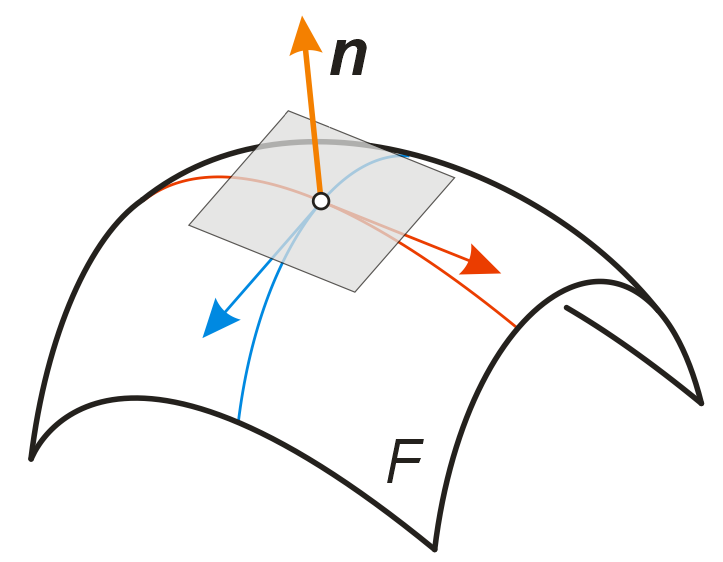
Die soeben berechneten Vektoren Fu und Fv legen die Richtungen von zwei Tangenten im Kugelpunkt P=F(u,v) fest. Der Richtungsvektor n der Flächennormalen steht zu diesen beiden Vektoren und lässt sich daher mit Hilfe des berechnen.
Mehrfachauswahl
Berechne das Kreuzprodukt der Vektoren
und
.
Wie lautet das richtige Ergebnis?
| |
| |
| |
Fassen wir zusammen:
1) Die partiellen Ableitungen (nach u bzw. v) sind Richtungsvektoren der Tangenten an die u- und v-Linien.
2) Der Normalvektor n wird mit Hilfe des Kreuzproduktes berechnet.
In unserem Beispiel berechnet sich dieser mit:
Multiple-Choice Wir berechnen nun den Einheitsvektor n0 der Flächennormalen.
Überlege bei den folgenden Aussagen, ob sie richtig oder falsch sind - versuche deine Wahl zu begründen und vergleiche mit dem Feedback.
|
Die Länge eines Vektors (x,y,z) berechnet sich als Summe der einzelnen Komponenten.
| |
|
Die Länge eines Vektors (x,y,z) berechnet sich als Produkt der einzelnen Komponenten.
| |
|
Die Länge eines Vektors (x,y,z) berechnet sich mit:
|
...Länge des Vektors n)
mit 1/(Länge des Vektors)
Wir erhalten das Offset einer Fläche analog zum Offset einer Kurve, indem wir auf den Flächennormalen einen konstanten Abstand d abtragen.
Das Offset einer Fläche berechnet sich daher mit:
In unserem Fall erhalten wir durch Einsetzen
und damit durch Zusammenfassen
Die Parallelflächen von Elipsoiden sind keine Ellipsoide!