Offset eines hyperbolischen Paraboloids
Vorwissen
Für die folgende Übung sind folgende Vorkenntnisse empfehlenswert:
- Parameterdarstellung von Flächen
- partielle Ableitungen
- Kreuzprodukt von Vektoren
- Einheitsvektoren (normierte Vektoren)
Ziele
In dieser Übung erarbeiten wir das Offset (Parallelfläche) eines hyperbolischen Paraboloids (HP).
Angabe eines HPs durch ein windschiefes Vierseit:
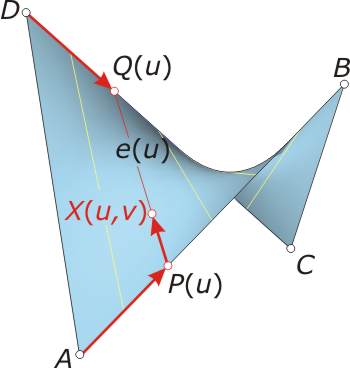
Legt man ein HP durch ein windschiefes Vierseit ABCD fest, so kann es folgendermaßen dargestellt werden:
F(u,v) = (1-v)(1-u) A + (1-v) u B + v(1-u)D + vu C
Diese Darstellung erhält man, indem man die zwei windschiefen Strecken AB und CD im selben Verhältnis teilt und entsprechende Punkte P auf AB und Q auf CD miteinander verbindet:
Dann hat P auf AB die Darstellung
Analoges gilt für Q auf DC :
Q(u) = (1-u) D + u C
Anm.: d.h. die Punkte P(u) und Q(u) mit demselben Parameterwert u entsprechen einander.
| Ein Punkt X auf PQ hat die Darstellung: | |
| X ... X(u,v) = P + v PQ = (1-v) P + v Q |
|
| Einsetzen von P(u) und Q(u) liefert somit: |
|
Mehrfachauswahl
Offset eines HPs
Zur Berechnung des Offsets eines Ellipsoids verwenden wir die folgende Parameterdarstellung
und berechnen die partiellen Ableitungen.
Welche der folgenden Antworten ist richtig?
| |
| |
| |
| |
| |
| |
Lücken-Aktivität
Verwende zum Ausfüllen des Lückentexts die Wörter:
parallel, windschief, normal, Kreuzprodukts, skalaren Produkts
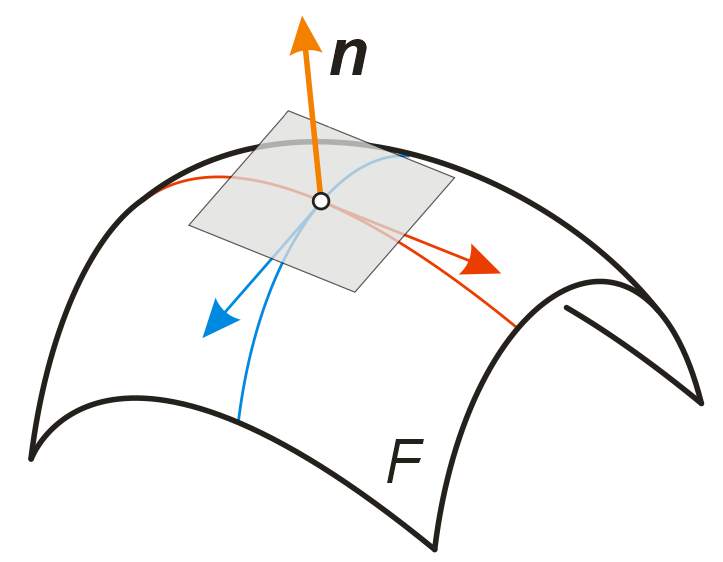
Die soeben berechneten Vektoren Fu und Fv legen die Richtungen von zwei Tangenten im Kugelpunkt P=F(u,v) fest. Der Richtungsvektor n der Flächennormalen steht zu diesen beiden Vektoren und lässt sich daher mit Hilfe des berechnen.
Mehrfachauswahl
Nun wählen wir für die Eckpunkte A,B,C,D des Angabevierseits folgende Werte:
A(1|1|-1), B(-1|1|1), C(1|-1|1), D(-1|-1|-1).
Damit erhalten wir die Vektoren
und
.
Berechne das Kreuzprodukt der Vektoren Fu und Fv. Wie lautet das richtige Ergebnis?
| |
| |
| |
Fassen wir zusammen:
1) Die partiellen Ableitungen (nach u bzw. v) sind Richtungsvektoren der Tangenten an die u- und v-Linien.
2) Der Normalvektor n wird mit Hilfe des Kreuzproduktes berechnet.
In unserem Beispiel berechnet sich dieser als:
Multiple-Choice Wir berechnen nun den Einheitsvektor n0 der Flächennormalen.
Überlege bei den folgenden Aussagen, ob sie richtig oder falsch sind - versuche deine Wahl zu begründen und vergleiche mit dem Feedback.
|
Die Länge eines Vektors (x,y,z) berechnet sich als Summe der einzelnen Komponenten.
| |
|
Die Länge eines Vektors (x,y,z) berechnet sich als Produkt der einzelnen Komponenten.
| |
|
Die Länge eines Vektors (x,y,z) berechnet sich mit:
|
berechnet sich mit:
...Länge des Vektors 
.
Wir erhalten das Offset einer Fläche analog zum Offset einer Kurve, indem wir auf den Flächennormalen einen konstanten Abstand d abtragen.
Das Offset einer Fläche berechnet sich daher mit:
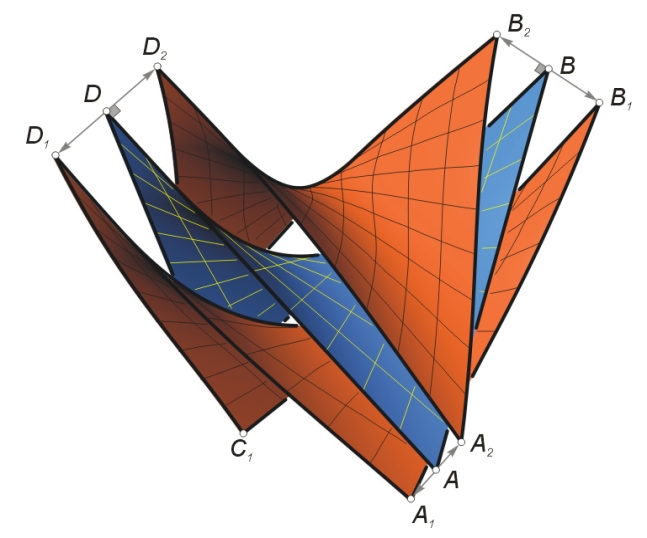In unserem Fall erhalten wir für d=4:
Die Parallelflächen von hyperbolischen Paraboloiden sind keine Regelflächen. Die geradlinigen Erzeugenden werden in krumme Parameterlinien übergeführt.