Navigation

1. Die kürzeste Verbindung
2. Die Loxodrome
3. Kartenentwürfe
4. Peilung
5. Ausblick: Weitere Navigationsverfahren

Literatur
 

Am 1. September 1983 ist durch einen Navigationsfehler eine Boeing 747 der Korean Air Lines über 600 Kilometer vom Kurs abgekommen und befand sich dann über militärischen Sperrgebiet der UdSSR. Dieser kleine Navigationsfehler kostete allen 269 Menschen an Bord das Leben. Rademacher beschreibt in [9] diesen tragischen Zwischenfall mitten im Kalten Krieg, der erst in jüngster Vergangenheit rekonstruiert werden konnte.

Auf welchen Wegen bewegt sich nun ein Flugzeug? Wahrscheinlich auf einer möglichst kurzen, schließlich soll ja Treibstoff gespart werden. Aber wie sieht die kürzeste Verbindung zweier Orte auf der Erdkugel überhaupt aus? Und kann ein Flugzeug leicht auf dieser kürzesten Route gesteuert werden? Wenn nein, welche Alternativen gibt es? Wie sehen die Kompromisse aus? Und wie kann man ein Flugzeug navigieren und seinen Aufenthaltsort feststellen, wenn man über den Wolken fliegt?
 
 

1. Die kürzeste Verbindung

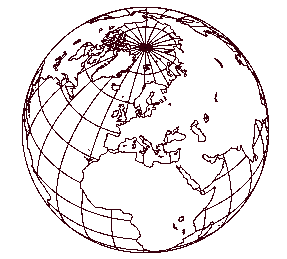
Durch zwei Punkte A und B einer Kugeloberfläche lassen sich unendlich viele Kleinkreise, aber nur ein Großkreis k legen. Jeder Kleinkreis, der in die Großkreisebene geklappt wird, hat kleineren Radius als der Großkreis und damit größere Krümmung. Daher stellt der Großkreisbogen zwischen A und B die kürzeste Verbindung beider Punkte dar. In diesem Zusammenhang ist auch die Bezeichnung Orthodrome üblich.

Bsp1: Es ist die Orthodrome zwischen Wien (16,2° Ost, 48,1° Nord) und New York (73,8° West, 40,6° Nord) zu ermitteln!

Anmerkung: Die Länge der Flugstrecke läßt sich mit Mitteln der ebenen oder sphärischen Trigonometrie berechnen und beträgt 6.784 km.

Als Richtungsangabe für Flug- oder Schiffsrouten dient der Kurswinkel. Darunter versteht man den Winkel zwischen Meridianen und Bewegungsrichtung. Er wird von der Nordrichtung aus über Ost von 0° bis 360° gezählt.

Zur Festlegung des Kurswinkels im Startpunkt eignet sich eine normale Axonometrie, wobei Kugelmittelpunkt (i.a. im Koordinatenursprung angenommen) und Startpunkt denselben Bildpunkt haben. Dann ist nämlich die Großkreisebene für die Flugroute immer projizierend und der Startkurswinkel kann einfach abgemessen werden.

Bsp 2: Es soll eine normale Axonometrie der Erdkugel so festgelegt werden, dass der Erdmittelpunkt und Wien (16,2° Ost, 48,1° Nord) denselben Bildpunkt haben. Daraus ist der Startkurswinkel für die Flugroute nach New York zu entnehmen.

Anleitung: Der Kugelmittelpunkt soll in den Koordinatenursprung fallen. In Grund- und Aufrissdarstellung kann der Sehstrahl für die Axonometrie (= Wien - Erdmittelpunkt) eingezeichnet werden und mittels zweier Seitenrisse projizierend gemacht werden. So legt man den 4. Riss eines geeigneten Bildspurdreiecks fest.

Lösung: Startkurswinkel a = ________°
 
 

2. Die Loxodrome

Der Weg entlang der Orthodrome ist zwar der kürzeste, hat jedoch den Nachteil, dass der Kurswinkel ständig geändert werden muß, was praktisch nicht durchführbar ist.

Eine Kurve auf der Kugel, die alle Meridiane unter demselben Winkel schneidet, heißt eine Loxodrome. Im allgemeinen nähert sich eine Loxodrome asymptotisch den Polen (Die Sonderfälle sind die Kurswinkel 0° und 180°, wo die Loxodrome mit einem Meridian zusammenfällt, bzw. 90° und 270°, wo die Loxodrome mit einem Breitenkreis zusammenfällt.). M.C. ESCHER stellt in [5, Seiten 231, 233] zwei Kugelbildern Loxodromenkurven dar.

Wählt man für die Flugroute aus Bsp 1 zwischen Wien und New York nicht die Orthodrome, sondern die Loxodrome, ergibt sich ein Kurswinkel von 263,3° und eine Entfernung von 7.147 km (vgl. [1], Seite 87f). Der Vorteil des konstanten Kurswinkels macht also einen um 363 km längeren Weg notwendig.

Im beiliegenden Software-Paket können zwei beliebige Orte aus einer Liste ausgewählt werden. Das Programm zeichnet dann Orthodrome und Loxodrome ein, gibt den Kurs für die Loxodromenbahn an und weist den Entfernungsunterschied aus.

In der Praxis werden die beiden Möglichkeiten insofern verbunden, dass man auf der Orthodrome einige Zwischenpunkte bestimmt und diese auf Loxodromenstücken ansteuert. Zur konstruktiven Lösung sind daher folgende Aufgaben zu bearbeiten:

Anlegen von Karten, auf denen entweder Großkreise oder Loxodrome einfach eingezeichnet werden können.

Festlegen der Orthodrome zwischen Anfangspunkt A und Zielpunkt Z sowie geeigneter Zwischenpunkte S₁, S₂, ..., S_n

Bestimmung des Kurswinkels des Loxodromenstückes von A nach S₁, von S₁ nach S₂, ..., von S_n nach Z.

Feststellen des Aufenthaltsortes (Peilung), um zu wissen, wann ein neuer Kurs aufgenommen werden muß

3. Kartenentwürfe

Zunächst soll gefordert werden, dass Großkreise im Kartenbild geradlinig erscheinen. Da alle Großkreisebenen den Kugelmittelpunkt enthalten, soll er als Projektionszentrum gewählt werden (gnomonische Projektion). Somit sind alle Großkreisebenen projizierend und die Orthodromenbilder geradlinig. Als Bildebene wählen wir eine geeignete Tangentialebene. Als Bilder der Breitenkreise treten in Abhängigkeit von Berührpunkt der Bildebene und Breitengrad die Kegelschnittstypen auf; im Sonderfall einer polständigen Karte (d.h. Bildebene ist die Tangentialebene in einem Pol) sind es konzentrische Kreise.

In dieser Karte kann nun die verbindende Orthodrome als geradlinige Verbindung eingezeichnet werden. Genauso kann man geeignete Zwischenpunkte wählen und deren Koordinaten ablesen.

Bsp 3.1: Die Flugstrecke von Wien nach New York ist einzuzeichnen und als Zwischenpunkte sollen die Schnittpunkte mit den Meridianen 15° West und 45° West gewählt werden.
 

Für die weitere Behandlung benötigt man einen Kartenentwurf mit neuen Eigenschaften: Nun sollen die Bilder der Loxodromen geradlinig verlaufen und zur Ablesung des Kurswinkel sollte Winkeltreue (Konformität) vorliegen.

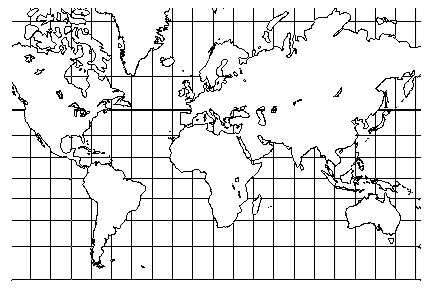
Falls es einen solchen Entwurf gibt, können bereits einige notwendige Bedingungen formuliert werden:

Da Breiten- und Längenkreise selbst Loxodrome sind, werden sie auf Geraden abgebildet. Aufgrund der Winkeltreue schneiden die Bildgeraden der Breitenkreise die Bildgeraden der Meridiane normal, bilden also ein rechtwinkeliges Gitternetz. Wegen der Parallelität der Bilder der Längenkreise und der Winkeltreue werden auch die von den Längen- und Breitenkreisen verschiedenen Loxodrome auf Geraden abgebildet.

Diese Bedingungen sind auch hinreichend (ohne Beweis), und ein solcher Entwurf wird nach dem lateinisierten Namen von Gerhard KREMER (1512-1594) MERCATOR-Karte oder Seekarte genannt.

Nun lässt sich die Navigationsaufgabe fortsetzen: In der MERCATOR-Karte werden die Punkte A, S₁, S₂, ..., S_n, Z eingetragen und die verbindenden Loxodromen als geradlinige Verbindung eingezeichnet. Die Kurswinkel der einzelnen Zwischenstücke lassen sich unmittelbar abmessen.

Bsp. 3.2: Es sind Wien, New York und die gewählten Zwischenpunkte einzutragen und die einzelnen Kurswinkel abzulesen.

Lösung: ________°, ________°, ________°
 
 

4. Peilung

Unter der Vielzahl von Peilungsmöglichkeiten sollen Fremdpeilung und Eigenpeilung genauer untersucht werden, weil diese konstruktiv gut durchführbar sind.

Bei der Fremdpeilung wird man von mindestens zwei Peilstellen P₁ und P₂, deren Koordinaten man genau kennt, zu einem bestimmten Zeitpunkt angepeilt. Als Ergebnis erhält man die Peilwinkel a _i := Ð NP_iS, also die Winkel zwischen den Meridianen durch die Peilstellen und der Verbindung zum Aufenthaltsort S (wiederum gemessen von der Nordrichtung über Ost von 0° bis 360°). Nun sind lediglich die beiden Verbindungslinien zum Aufenthaltsort ( = Großkreise!) zu schneiden, um seinen Aufenthaltsort festzustellen.
Die Koordinaten lassen sich aber auch mit Mitteln der sphärischen Trigonometrie berechnen (vgl. [1], Seite 68f).

Zur konstruktiven Auswertung wählt man keine Großkreiskarte (obwohl dort die Großkreise geradlinig verlaufen würden), sondern eine MERCATOR-Karte, deren Winkeltreue man ausnützen will. Wie kann man aber nun einen Großkreis festlegen?

Der Großkreis wird durch seine Tangenten in den Endpunkten S und P₁ ersetzt. Die S und P₁ verbindende Orthodrome und Loxodrome schneiden einander unter den Winkeln u_S bzw. u₁. Mit hinreichender Genauigkeit kann man u_S = u₁ = u setzen und durch die Näherung

bestimmen, wobei D l der Unterschied der Längengrade und j _m der Mittelwert der Breitengrade von S und P₁ sind (vgl. [1], Seite 99ff). u wird als Loxodromenbeschickung bezeichnet.

Zur Berechnung von u benötigt man also die Koordinaten des Aufenthaltsortes, den man aber erst bestimmen möchte! Also geht man von einem ungefähren Aufenthaltsort (Loggeort oder Koppelort, abgekürzt mit Og) aus, der aufgrund von Geschwindigkeit und Kurs angegeben wird. u wird nun für Og berechnet. In der Karte wird bei P₁ der von der Peilstelle angegebene Winkel a₁ und die Loxodromenbeschickung u eingetragen. Dabei ist zu beachten, dass die Loxodrome immer näher zum Äquator liegt als die zugehörige Orthodrome. Die Loxodrome kann nun geradlinig eingezeichnet werden. Sie schneidet den Meridian des Koppelpunktes im Leitpunkt L₁. Wenn jetzt in L₁ der Winkel u entgegengesetzt eingetragen wird, erhält man wieder die Tangente an den Großkreis. Dieses Verfahren muss noch bezüglich der zweiten Peilstelle P₂ durchgeführt werden, womit man schließlich den Standort S als Schnittpunkt der beiden Tangenten erhält.

Bsp. 4: (nach [1], S. 102)

Folgende Daten sind gegeben:

P₁ (64,6° West, 32,5° Nord), Peilwinkel a₁ = 126°

P₂ (25,2° West, 17° Nord), Peilwinkel a₂ = 261°

Als Loggeort nehmen wir einen sehr „schlecht" gekoppelten Ort an: Og (40° West, 13° Nord).

Berechnung der Loxodromenbeschickungen u₁ (bezüglich P₁) und u₂ (bezüglich P₂):

D l ₁ = 24,6° j _m1 = 22,8° Þu₁ = 12,3° sin 22,8° = 4,8°

D l ₂ = 14,8° j _m2 = 15° Þu₂ = 7,4° sin 15° = 1,9°

Lösung: Standort S ( _____° ____ , _____° ____ )
 

Bei der Eigenpeilung werden dagegen vom Standort S aus die Richtungen zu mindestens zwei Kreisfunkfeuern F₁ und F₂, deren Koordinaten man genau kennt, gemessen. Man erhält die Peilwinkel a_i := Ð NSF_i, also Winkel zwischen dem Meridian durch S und der Verbindung zum Kreisfunkfeuer ( = wieder ein Großkreis!).

Alle Orte, die zu einem Kreisfunkfeuer denselben Peilwinkel aufwiesen, liegen auf einer sogenannten Azimutgleiche. Um den Aufenthaltsort zu bestimmen, müssen nun für beide Kreisfunkfeuer die Azimutgleichen bestimmt und geschnitten werden. Rechnerisch entsteht hier ein erheblicher Aufwand, denn es müssen Gleichungen 8. Grades gelöst werden!

Die konstruktive Auswertung erfolgt wiederum auf einer MERCATOR-Karte und die Azimutgleiche wird ebenfalls durch die Tangente ersetzt. Orthodrome und Azimutgleiche schneiden einander in S unter dem Winkel n , wobei die Azimutgleiche immer äquatorwärts zur Orthodrome liegt. n lässt sich in für die Praxis ausreichender Genauigkeit durch

berechnen, wobei j die geographische Breite von S ist. Ein Vergleich mit der Formel für die Loxodromenbeschickung u zeigt bei nicht allzu großem Unterschied von j und j _m und großem j , dass

gilt (Bemerkung). Insgesamt liegen also die Loxodrome mit Winkel u und die Azimutgleiche mit Winkel 2u äquatorwärts von der Orthodrome, daher ist der Winkel zwischen der Loxodrome und der Azimutgleiche ebenfalls u. Damit kann die Tangente an die Azimutgleiche durch Abtragen der Loxodromenbeschickung u von der (in der MERCATOR-Karte geradlinigen) Loxodrome gefunden werden.

Zur Berechnung von u dient wiederum ein Loggeort Og. Mit Og und dem Winkel a ₁ zum Funkfeuer F₁ lässt sich die Loxodrome von F₁ aus einzeichnen. Als Schnitt mit dem Meridian durch Og ergibt sich der Leitpunkt L₁, wo die Tangente an die Azimutgleiche eingezeichnet wird. Durch Wiederholen dieses Verfahrens für das Funkfeuer F₂ erhält man schließlich den Aufenthaltsort S.

Bsp 5: (nach [1], S. 111)

Folgende Daten sind gegeben:

F₁ (64,6° West, 32,5° Nord), angepeilt unter a₁ = 328,5°

F₂ (25,2° West, 17° Nord), angepeilt unter a₂ = 74,8°

Als Loggeort nehmen wir einen sehr „schlecht" gekoppelten Ort an: Og (48° West, 10° Nord).

Berechnung der Loxodromenbeschickungen u₁ (bezüglich F₁) und u₂ (bezüglich F₂):

D l ₁ = 16,6° j _m1 = 21,3° Þu₁ = 8,3° sin 21,3° = 3,0°

D l ₂ = 22,8° j _m2 = 13,5° Þu₂ = 11,4° sin 13,5° = 2,7°

Lösung: Standort S ( ______° ____ , _____° ____ )
 
 

5. Ausblick: Weitere Navigationsverfahren

Das sogenannte Omega-Verfahren bedient sich acht gleichmäßig auf der Erde verteilter Sendestationen und wurde erst zu Beginn der 80er-Jahre technisch voll realisiert.

Zur Bestimmung einer Standlinie für den Aufenthaltsort S benötigt man zwei dieser Sendestationen, aufgrund deren geschickter Verteilung und großen Reichweite können aber von jedem Ort der Erde 4 bis 6 Omegastationen empfangen werden und somit 3 bis 5 unabhängige Standlinien bestimmt werden.

Die Stationen senden frequenz- und phasengleiche Wellen aus. Nun wird die Phasendifferenz gemessen, die an all jenen Orten gleich groß ist, an denen die Differenz der Abstände zu den Sendestationen gleich ist. In der Ebene sind solche Kurven Hyperbeln mit den Sendestationen als Brennpunkte, und auf der Kugel spricht man von „sphärischen Hyperbeln". Umgekehrt liefert jedoch gleiche Phasendifferenz eine ganze Schar von Hyperbeln, daher wird in der Praxis eine niedrige Frequenz gewählt, woraus eine große Wellenlänge folgt und sich relativ große Abstände für benachbarte Hyperbeln ergeben (ca. 13 km). Man muß also während der Fahrt die Zahl der überschrittenen Hyperbeläste z.B. zur Phasendifferenz 0 bestimmen, um zu wissen, in welchem Hyperbelstreifen man sich befindet.

Es sei noch angemerkt, daß der Ausdruck sphärische Kegelschnitte insofern berechtigt ist, als diese Kurven auch als Durchdringungslinien von Kugel und Kegel entstehen.

Für genauere Ausführungen siehe [1] S.77ff. und [3].
 

Literatur

Internet:

                   http://www.astro.ch/atlas/

                    viele nützliche Informationen über die Erdkugel, geographische Koordinaten, ...