Die
Parabel in Physik und Geometrie
Die Wurfparabel
1.
Historisches
2.
Das physikalische Problem
3.
Eine einfache Herleitung der Wurfkurve
4.
Eine anspruchsvolle Herleitung der Wurfkurve
5.
Physikalische Folgerungen
6. Beispiel
Basketball
Die Planetenbewegung
7. Historisches
8.
Das physikalische Problem
9.
Eine Herleitung der Planetenbewegung
10.
Beispiel Komet
Vorschläge
für einen projektartigen Unterrichsablauf
Literatur
Die Wurfparabel
1.
Historisches ([1] und
[2])
Die Frage „Warum fällt der Apfel zu Boden?" - dh. die Frage nach
Ursache und Form einer Bewegung - beschäftigte nicht erst Isaac Newton,
sondern schon griechische Philosophen.
Unter einer Bewegung verstand man im antiken Griechenland einen Prozeß,
der
-
einen natürlichen oder gewaltsamen Antrieb benötigt (Aristoteles)
oder
-
durch eine allmählich abnehmende Kraft (-diese heißt Impetus-)
gesteuert wird (Philoponos).
Daß diese Modelle fast 2 Jahrtausende unumstritten blieben, liegt
an der strengen Trennung von Mathematik und Physik. Es ist eine Ironie
des Schicksals, daß gerade Galilei
Galileo, der diese Konzepte einer Bewegung erstmals durch eine mathematische
Theorie zu stützen versuchte, zugleich einer gänzlich anderen
Betrachtungsweise den Weg ebnete:
Anfang des 17. Jahrhunderts formulierten der Mathematiker Rene
Descartes und der Physiker Christian Huygens eine neue Theorie: Bewegung
sei ein Zustand, dessen Änderung eine Ursache benötige. Während
-
Descartes und Huygens den Stoß als Ursache ansahen,
-
erkannte Isaac Newton (1642-1727) die Kraft als Ursache jeglicher Bewegungsänderung.
Isaac Newton, dem Begründer der klassischen Physik, gelang es, die
bislang getrennt untersuchten Phänomene „Wurfbewegung" und „Planetenbewegung"
unter Verwendung des Kraftfeldbegriffs einheitlich zu behandeln und auf
dasselbe Prinzip „Gravitation" zurückzuführen.
Dabei berief er sich auf das von ihm entdeckte Allgemeine
Gravitationsgesetz. Wir folgen nun Newtons Spuren.
2.
Das physikalische Problem ([4],
[6]
und [7])
Wir wollen die Wurfbahn eines Objekts unter Einfluß der Schwerkraft
untersuchen. Aufgrund von Beobachtungen vermuten wir:
Die Art der Wurfkurve ist abhängig von
-
der äußeren Form, Dichte und Masse m des Objekts,
-
der Erdbeschleunigung (Schwerkraft),
-
dem Reibungswiderstand (Luftwiderstand),
-
der Starthöhe h0
-
der Startgeschwindigkeit v0 und
-
dem Startwinkel j0
gegen die Erdoberfläche.
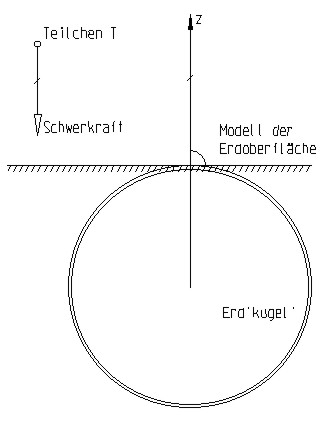 Da es kaum
möglich ist, alle die Wurfbahn beeinflussenden Parameter in eine möglichst
einfache Universalformel einzubringen, treffen wir einige Vereinfachungen
(Idealisierungen):
Da es kaum
möglich ist, alle die Wurfbahn beeinflussenden Parameter in eine möglichst
einfache Universalformel einzubringen, treffen wir einige Vereinfachungen
(Idealisierungen):
-
Wir vernachlässigen Form und Dichte des Objekts und betrachten die
Bahnkurve des Schwerpunkts, dh. des Teilchens T mit Masse
m.
-
Wir ersetzen die gekrümmte Erdoberfläche lokal durch eine Tangentialebene
p1.
-
Wir setzen voraus, daß auf jedes Teilchen T eine gegen die Standebene
p1
gerichtete
Schwerkraft
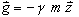 wirkt.
Die Gravitationskonstante
g» 9.81 ms-2
ist der Durchschnittswert ortsabhängiger, experimentell bestimmter
Meßwerte. Alle Schwerkraftvektoren bilden ein homogenes Parallelkraftfeld.
wirkt.
Die Gravitationskonstante
g» 9.81 ms-2
ist der Durchschnittswert ortsabhängiger, experimentell bestimmter
Meßwerte. Alle Schwerkraftvektoren bilden ein homogenes Parallelkraftfeld.
-
Wir vernachlässigen den Luftwiderstand. (Auch diesen müssten
wir als ein Vektorfeld erklären!)
Nach diesen Vorbereitungen fällt es nicht schwer, die Wurfbahn als
Parabel zu identifizieren:
3.
Eine einfache Herleitung der Wurfkurve ([5],
[6] und [4])
Wir setzen neben unseren Vereinbarungen die 3 Newtonschen Gesetze und
das Unabhängigkeitsprinzip
voraus und zerlegen die Gesamtbewegung in 2 Teile:
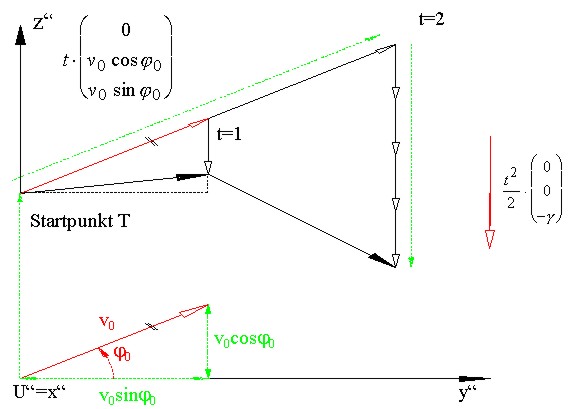
-
Führungsbewegung: Wird das Teilchen T mit der konstanten Startgeschwindigkeit
v0 unter dem Startwinkel j0
abgeschossen, so bewegt es sich ohne Berücksichtigung der Schwerkraft
unbeschleunigt geradlinig und gehorcht der Formel „zurückgelegter
Weg s = Geschwindigkeit v0 ·
Zeit t"
-
Fallbewegung: Fällt das Teilchen T ohne Berücksichtigung von
Startgeschwindigkeit und Startwinkel, dann wird es durch die Erdanziehungskraft
gleichmäßig beschleunigt und gehorcht somit der Formel
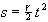 .
Der zurückgelegte Weg wächst mit dem Quadrat der verstrichenen
Zeit.
.
Der zurückgelegte Weg wächst mit dem Quadrat der verstrichenen
Zeit.
-
Die tatsächliche Wurfbewegung entsteht als Überlagerung (Vektoraddition)
dieser beiden Teilbewegungen. Bei der erzeugten Wurfkurve handelt es sich
um eine ebene Kurve.
Im Gegensatz zur üblichen Praxis bestimmen wir die Gleichung der Wurfkurve
in einem y-z-Koordinatensystem. Dadurch soll die räumliche Lage der
Kurve betont werden.
Die Parameterdarstellung der Kurve lautet damit (bei Vernachlässigung
der Starthöhe h0)
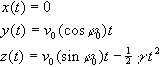 .
.
Die Bahngleichung ergibt sich nach Eliminieren des Zeitparameters t
unter Verwendung von
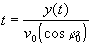
als
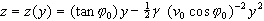 .
.
Diese Gleichung 2. Grades beschreibt, wie allgemein bekannt, eine Parabel.
Im nächsten Abschnitt entwickeln wir dieselbe Gleichung unter anderen
Voraussetzungen; daher verzichten wir an dieser Stelle auf genauere Untersuchungen.
Die Abhängigkeit der Parabelbahn von den Parametern v0
und j0 kann etwa durch ein Algebraprogramm
visualisiert werden. (Genaueres dazu findet sich in [4])
4. Eine anspruchsvolle Herleitung
der Wurfkurve ([5])
Wir verzichten auf das Unabhängigkeitsprinzip und leiten die Bewegungsgleichung
aus dem abstrakten Begriff des Parallelkraftfelds und unter Vermeidung
allzu anschaulicher Betrachtungen ab. Diese Methode hat gegenüber
der naiven Betrachtung in 3. den Vorteil, auf beliebige Kraftfeldtypen,
so etwa der Zentralkraft (siehe Planetenbewegung), anwendbar zu sein.
Wir betrachten wieder ein Teilchen T mit Masse m und Ortsvektor 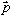 (in einem räumlichen Koordinatensystem mit Einheitsvektoren
(in einem räumlichen Koordinatensystem mit Einheitsvektoren 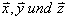 ),
welches während des Wurfs durch die Schwerkraft beschleunigt wird.
Nach dem 2. Newtonsche Gesetz „Kraft
),
welches während des Wurfs durch die Schwerkraft beschleunigt wird.
Nach dem 2. Newtonsche Gesetz „Kraft 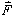 =Masse
m · Beschleunigung
=Masse
m · Beschleunigung 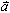 "
wirkt auf das Teilchen die Kraft
"
wirkt auf das Teilchen die Kraft
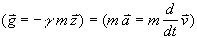 .
.
Wir vereinfachen diese Vektorgleichung zu
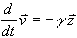 .
.
Nach einmaliger Integration nach t erhalten wir den Geschwindigkeitsvektor
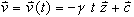 ,
,
worin 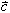 einen konstanten
Vektor (Integrationskonstante) darstellt. Unter Verwendung der Startwerte
j0
und v0 und der daraus resultierenden Startbedingung
einen konstanten
Vektor (Integrationskonstante) darstellt. Unter Verwendung der Startwerte
j0
und v0 und der daraus resultierenden Startbedingung
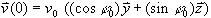
errechnen wir die Konstante 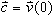 .
Wir integrieren
.
Wir integrieren
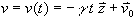
und erhalten eine Parameterdarstellung der Wurfkurve als
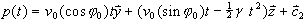 .
.
Bei 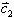 handelt es sich
um eine Schiebkonstante. Berücksichtigen wir die Starthöhe h0,
so erhalten wir die ausführlich geschriebene Parameterdarstellung
handelt es sich
um eine Schiebkonstante. Berücksichtigen wir die Starthöhe h0,
so erhalten wir die ausführlich geschriebene Parameterdarstellung
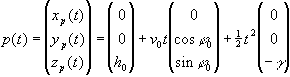 .
.
Wir vernachlässigen die Wurfhöhe (h0=0)
und erhalten eine die Wurfbahn beschreibende Gleichung als
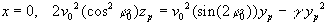 .
.
Wir wenden auf diese Kurve eine Schiebung (metrische Hauptachsentransformation
mit neuen Koordinaten x0,y0,z0)
an und erhalten die Gleichung einer nach unten geöffneten Parabel
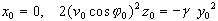
mit lotrechter Achse und Parabelparameter 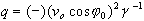 .
.
5.
Physikalische Folgerungen ([5])
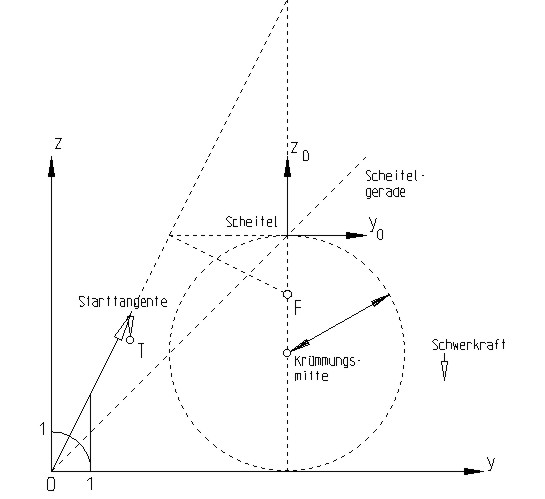
-
Die Masse des Objekts hat auf die Flugbahn keinerlei Auswirkung.
-
Die Anfangsgeschwindigkeit v0 errechnet
sich aus dem Scheitelkrümmungsradius q der Wurfparabel (entspricht
dem Parabelparameter) als
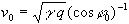 .
Damit ist es prinzipiell möglich, aus etwa einer Stroboskopaufnahme
bei Kenntnis des Startwinkels durch Messung des Parabelparameters auf die
Startgeschwindigkeit zu schließen.
.
Damit ist es prinzipiell möglich, aus etwa einer Stroboskopaufnahme
bei Kenntnis des Startwinkels durch Messung des Parabelparameters auf die
Startgeschwindigkeit zu schließen.
-
Wir bestimmen die Koordinaten des an höchster Stelle gelegenen Parabelscheitels
S: Da seine z-Koordinate maximal sein muß, führt Differenzieren
und „Null-Setzen" der 3. Komponente
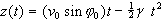 zu
zu 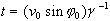 . Zu
diesem Zeitpunkt durchläuft das Teilchen P den Kurvenscheitel S mit
den Koordinaten
. Zu
diesem Zeitpunkt durchläuft das Teilchen P den Kurvenscheitel S mit
den Koordinaten 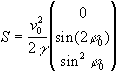 .
.
-
Setzen wir konstanten Abschußwinkel
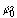 voraus und betrachten wir die Schar aller zu verschiedenen Startgeschwindigkeiten
v0 gehörigen Wurfparabeln, dann liegen
alle Parabelscheitel
auf der „Scheitel"geraden
voraus und betrachten wir die Schar aller zu verschiedenen Startgeschwindigkeiten
v0 gehörigen Wurfparabeln, dann liegen
alle Parabelscheitel
auf der „Scheitel"geraden 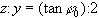 .
.
-
Sind Start- und Landehöhe gleich , etwa z=0, dann folgt aus
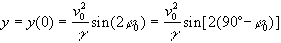 die bekannte Aussage: „Komplementäre Wurfwinkel liefern dieselbe Weite."
die bekannte Aussage: „Komplementäre Wurfwinkel liefern dieselbe Weite."
-
Wir verwenden die obige Formel und erkennen aufgrund der Maxima der Sinusfunktion:
„Die größte Wurfweite wird bei j0=45°
erreicht und beträgt
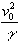
."
6.
Beispiel Basketball ([5])
Im folgenden wird das DG-Arbeitsblatt
„Basketball 1" zum Thema Wurfparabel besprochen.
Eine weitere, komplett analog zu lösende Aufgabe „Basketball 2"
ist beigelegt:
Basketball 1:Ein Basketballer
wirft einen Ball aus der Position W mit Wurfwinkel 40° (=1.Böschungswin-kel)
so, daß der Ball zuerst das Brett im Punkt B trifft und danach in
den Korb K fällt.
Beantworte:
Wo liegt der Reflexionspunkt B?
Wo liegt der Scheitel S der Wurfkurve?
Mit welcher Geschwindigkeit muß der Ball
abgeworfen werden, um diese Bahn einzuhalten?
Notwendiges Basiswissen:
-
Nur die Schwerkraft (homogenisiert, gegen die Grundrißebene gerichtet)
und die Startgeschwindigkeit beeinflussen die Wurfbahn.
-
Es gilt das Unabhängigkeitsprinzip der Mechanik. (Veranschaulichung
durch Vektoren)
-
Die Wurfkurve ist eine nach unten geöffnete Parabel mit lotrechter
Achse.
-
Das Reflexionsgesetz am ebenen Spiegel lautet „Einfallswinkel=Austrittswinkel".
Zur Lösung des Beispiels müssen folgende räumliche Überlegungen
angestellt werden:
-
Die Wurfbahn des Balls (genauer: seines Schwerpunkts) besteht aus zwei
Teilen; der erste reicht vom Abwurfort W bis zum Reflexionspunkt B am Brett,
der zweite von dort bis zur Korbmitte K (und darüber hinaus). Wir
verlängern den ersten Kurventeil p1 über B hinaus:
Der zweite Teil p2=p1s entsteht aus dem ersten durch
Spiegelung am Brett.
-
Wir spiegeln die Korbmitte K am Brett und erhalten den Punkt Ks.
Die Bahnebene von p1 ist lotrecht und daher durch W und Ks
bereits eindeutig bestimmt.
-
Die Starttangente t liegt in dieser Bahnebene und ist gegen die Standebene
40° geneigt. („Passende" Lösung auswählen!)
-
Die Wurfparabel p1 ist durch das Linienelement (W,t), dem Punkt
Ks und der lotrechten Achsenrichtung eindeutig bestimmt. (Beweis:
Parabelkonstruktion nach Domkowitsch.) Bemerkenswert ist, daß der
Scheitel der Raumparabel auf den Scheitel der Aufriß- bzw. Kreuzrißparabel
abgebildet wird. (Beweis: Parabelachse ist 2. und 3. Hauptgerade)
-
Der Reflexionspunkt B ist der Schnittpunkt der Parabel p1 mit
p2 und dem Brett. Er liegt auf der lotrechten Schnittgeraden
der Bahnebene von p1 und der Ebene des Bretts.
-
Aus der Kenntnis von Wurfwinkel und Parabelparameter (bzw. Scheitelkrümmungsradius)
kann die Startgeschwindigkeit nach 5. berechnet werden.
Zur konstruktiven Lösung des Beispiels sind folgende Grundoperationen
notwendig:
-
Konstruktion in Grund-, Auf- und Kreuzriß
-
Normale Lage Gerade-Ebene (Spiegelung von K)
-
Länge einer Strecke (Spiegelung von K)
-
Schnittaufgabe Ebene-Ebene (Bestimmung der lotrechten Trägergeraden
von B)
-
Eine projiziende Ebene durch einen Seitenriß oder eine Paralleldrehung
in Hauptlage bringen (Festlegung der Tangente t; Bestimmung des Parabelparameters)
-
Parabelkonstruktion aus 2 Linienelementen
-
Konstruktion eines Schnittpunkts einer Parabel mit einer Durchmessergeraden
(Bestimmung des Reflexionspunkts B)
-
Konstruktion des Scheitelkrümmungskreises einer Parabel
-
Schnittaufgabe Gerade-Ebene (Konstruktion der Tangente im Punkt K der Parabel
p2)
Die Planetenbewegung
7. Historisches
([1]
und [2])
Schon in der Antike beschäftigten sich Gelehrte mit den Himmelskörpern.
Während die Beobachtung des Sternenhimmels zuerst aus rein religiösen
Gründen (Babylonien, etwa 800 v.Chr.) geschah, bemühten sich
Gelehrte schließlich um die Lösung folgender Fragen:
-
Auf welchen Bahnen bewegen sich die Planeten?
-
Warum bewegen sich die Planeten?
-
Steht die Erde still oder bewegt sie sich ?
Über zwei Jahrtausende lang versuchten Wissenschaftler, das Geheimnis
der Planeten vorwiegend durch Beobachtung und von religiöser Überzeugung
geleitet zu ergründen. So „mußten" etwa die Planetenbahnen Kreisbahnen
sein, weil der Kreis in seiner Symmetrie „göttlich" wäre.
Es wurden folgende Theorien zuerst befürwortet, dann geprüft
und schließlich verworfen:
-
Babylon, 800 v.Chr.: Die Erde ruht in der Weltmitte, um die Fixsterne und
Planeten rotieren. (Geozentrisches Weltbild)
-
Pythagoreer: Erde, Gegenerde und die Planeten umkreisen das Zentralfeuer.
-
Herakleides von Pontos, 400 v.Chr.: Sonne und Erde laufen um die Weltmitte.
-
Aristarchos von Samos, 280 v.Chr.: Planeten umkreisen die Sonne. (Heliozentrisches
Weltbild)
-
Ägyptisches System, 300 v.Chr.: Die Erde ist die Weltmitte und wird
von Mond und Sonne umkreist; alle anderen Planeten umkreisen die Sonne.
-
Ptolemaios, 150 n.Chr.: Alle Planeten umkreisen die Erde auf Trochoidenbahnen.
Die scheinbar rückläufige Bewegung mancher Planeten begründet
er durch Epizykel.
-
Nikolaus Kopernikus (1473-1543) konnte die scheinbare Rückläufigkeit
mancher Planeten im heliozentrischen Weltbild ohne Verwendung von Epizykeln
hinreichend genau erklären.
-
Galilei Galileo beobachtete mit einem eigens gebauten Fernrohr Sonnenflecken
und die Venusphasen. Als er „seine" Rechtfertigung des kopernikanischen
Systems „Dialog über die beiden hauptsächlichen Weltsysteme,
das ptolemaische und das kopernikanische" veröffentlichte, wurde er
in einem Prozeß 1632 zum Widerruf seiner Ideen gezwungen.
-
Johannes Kepler (1571-1630) versuchte zuerst, das kopernikanische System
unter Verwendung „konzentrischer" Polyeder zu begründen. Nach umfangreichen
Studien und Beobachtungen beim kaiserlichen Hofastronom Tycho Brahe in
Prag formulierte er eine neue, durch Beobachtung gestützte Theorie
in den 3 Keplerschen
Gesetzen.
-
Isaak Newton gelang schließlich die mathematische Begründung,
d.h. der Beweis der
Keplerschen Gesetze.
8.
Das physikalische Problem ([5],
[6]
und [7])
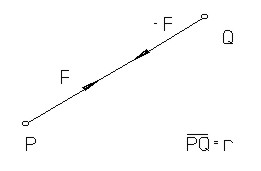
Wir setzen das Allgemeine Gravitationsgesetz von Isaac Newton voraus:
Zwei Massepunkte P und Q ziehen einander mit der Kraft 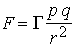 an, die nur von den Massen p und q sowie dem gegenseitigen Abstand der
Punkte P und Q abhängt. G
ist eine Naturkonstante und beträgt
etwa G = 6,673 10-11 Nm2/kg2.
an, die nur von den Massen p und q sowie dem gegenseitigen Abstand der
Punkte P und Q abhängt. G
ist eine Naturkonstante und beträgt
etwa G = 6,673 10-11 Nm2/kg2. |
|
Wir betrachten einen Himmelskörper, der in das Schwerefeld einer
Sonne eintritt. Die Art der neuen Flugbahn ist abhängig von
-
Form, Dichte und Masse m des Himmelskörpers,
-
der Entfernung zur Sonne („Startdistanz"),
-
der momentanen Bewegungsrichtung („Startrichtung") und -geschwindigkeit
(„Startgeschwindigkeit")
-
der Masse der Sonne,
-
der Naturkonstante G ,
-
der Anziehungskraft der Sonne
-
sowie der Anziehungskräfte weiterer Himmelskörper, die mit dem
Himmelskörper in Wechselwirkung treten.
Um zu einprägsamen Ergebnissen zu gelangen, vernachlässigen wir
Form und Dichte des Himmelskörpers und ersetzen ihn durch einen Massepunkt
(Schwerpunkt). Außerdem berücksichtigen wir keine weiteren Wechselwirkungen
mit anderen Himmelskörpern.
Die Gesamtbewegung des Teilchens läßt sich auf folgende Weise
in 2 Teilbewegungen zerlegen:
-
Führungsbewegung: Zu jedem Zeitpunkt bewegt sich das Teilchen ohne
Berücksichtigung der Anziehungskraft unbeschleunigt geradlinig.
-
Fallbewegung gegen das Kraftzentrum Sonne: Das Teilchen fällt gleichmäßig
beschleunigt in Richtung Sonne.
-
Die tatsächliche Flugbewegung entsteht als Überlagerung (Vektoraddition)
dieser beiden Teilbewegungen. Bei der Kurve handelt es sich eine ebene
Kurve.
9.
Eine Herleitung der Planetenbewegung ([5])
Da die mathematische Behandlung der Bewegungsbahnen Kenntnisse über
das Lösen von Differentialgleichungen 2. Ordnung verlangt, beschränken
wir uns auf eine skizzenhafte Beschreibung der Herleitung:
Im Gegensatz zur Wurfbewegung im homogenen Parallelkraftfeld wirken
nun alle Kraftvektoren in Richtung Kraftzentrum; wir sprechen daher von
einem homogenen Zentralkraftfeld und definieren:
Das Vektorfeld 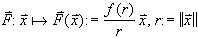 heißt homogenes Zentralkraftfeld. Ist f(r)<0, dann heißt
das Feld anziehend, ansonsten abstoßend.
heißt homogenes Zentralkraftfeld. Ist f(r)<0, dann heißt
das Feld anziehend, ansonsten abstoßend.
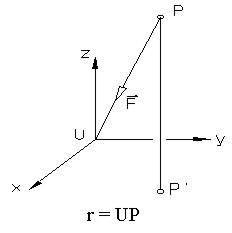
Da die Anziehungskraft nur vom Abstand des Punktes vom Zentrum abhängt,
liegt die Verwendung von Polarkoordinaten nahe. |
|
Wir verwenden folgende Kenntnisse:
(Nachzulesen in [5])
-
Unter Einfluß eines homogenen Zentralkraftfelds durchläuft jeder
Punkt eine ebene Bahn.
-
Der Ortsvektor des Punktes P überstreicht zu gleichen Zeiten gleiche
Flächen. (Flächensatz)
-
Die Bewegungsgleichungen eines Massepunkts P mit der Masse m und den Polarkoordinaten
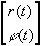 lauten
lauten  .
.
-
Unter Einfluß der Zentralkraft f(1/u), 1/u:=r wird die Bahn des Punktes
P durch die Differentialgleichung
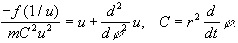
beschrieben.
In unserem Fall lautet der Kraftbetrag 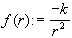 ;
die Konstante k ist Produkt der Konstanten G
, p und q. Wir substituieren r=1/u und setzen f(1/u) in die Bewegungsgleichung
ein. Die entstehende Differentialgleichung
;
die Konstante k ist Produkt der Konstanten G
, p und q. Wir substituieren r=1/u und setzen f(1/u) in die Bewegungsgleichung
ein. Die entstehende Differentialgleichung
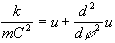
wird durch
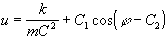
mit den Konstanten C1 und C2 (-bewirkt eine Drehung
um das Zentrum, wird daher vernachlässigt-) gelöst. Insgesamt
ergibt sich unter Verwendung der Abkürzungen
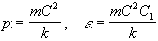
die Polargleichung
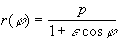
eines Kegelschnitts mit numerischer Exzentrizität e
. Unter Verwendung der Beziehung
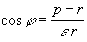
ergibt sich die Gleichung
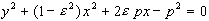 .
.
|
Bei 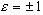 handelt es sich um eine Parabel mit linearer Exzentrizität p/2, ansonsten
um eine Ellipse oder Hyperbel mit halben Haupt- und Nebenachsenlängen
handelt es sich um eine Parabel mit linearer Exzentrizität p/2, ansonsten
um eine Ellipse oder Hyperbel mit halben Haupt- und Nebenachsenlängen 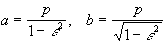 .
Im Falle einer Hyperbel ist b imaginär. Die lineare Exzentrizität
beträgt e=ae . In allen Fällen ist
das Kraftzentrum S ein Brennpunkt des Bahnkegelschnitts. .
Im Falle einer Hyperbel ist b imaginär. Die lineare Exzentrizität
beträgt e=ae . In allen Fällen ist
das Kraftzentrum S ein Brennpunkt des Bahnkegelschnitts. |
Zusammenfassend gilt:
Unter Einfluß einer zum Abstandsquadrat indirekt proportionalen
Zentralkraft beschreibt jedes Teilchen eine Kegelschnittsbahn. Ein Brennpunkt
dieser Bahn fällt in das Kraftzentrum S.
Der Parabelfall stellt den Übergang zwischen Ellipsen- und Hyperbelfall
dar und ist daher meist nur von theoretischem Interesse.
Bem.: Wurfparabel und Planetenbewegung sind zwei verschiedene
modellartige „Realisierungen" desselben Phänomens Bewegung. Beschreibt
man die Fallbewegung gegen die Erdoberfläche nämlich mit dem
genaueren Modell der Zentralkraft, so bewegt sich der Körper auf einer
Wurfellipse.
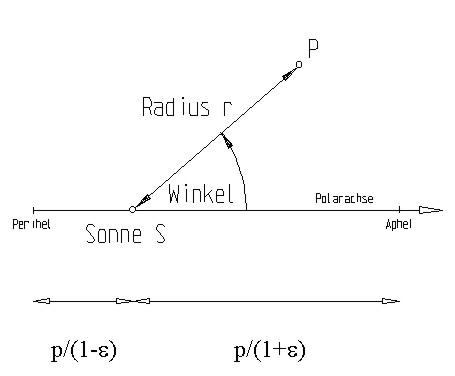
10.
Beispiel Komet ([5])
Im folgenden wird das DG-Arbeitsblatt „Komet 1" zum Thema Planetenbewegung
besprochen. Eine weitere, komplett analog zu lösende Aufgabe „Komet
2" ist beigelegt.
Komet 1: Ein Komet
bewegt sich auf parabolischer Bahn im Zentralkraftfeld der Sonne S. Von
der Bahn k sind momentane Position K und momentane Flugrichtung t (1.Hauptlage)
bekannt. Bestimme den kürzsten Abstand Komet-Sonne (Die Position heißt
Perihel bzw. Perigäum).
Hinweis: Es wird empfohlen, die Außrißparabel durch
3 Linienelemente festzulegen.
Notwendiges Basiswissen:
-
Die Anziehungskraft ist umgekehrt proportional zum Abstandsquadrat.
-
Alle Schwerkraftvektoren weisen zum Kraftzentrum Sonne.
-
Unter Einfluß dieses Krafttyps bewegen sich Himmelskörper auf
Kegelschnitten.
Zur Lösung des Beispiels müssen folgende räumliche Überlegungen
angestellt werden:
-
Die Bahn eines Kometen entspricht nur näherungsweise einer Parabel.
-
Die momentane Bewegungsrichtung t des Kometen wird in der Praxis durch
eine zwei benachbarte Kometenpositionen verbindende Sehne angenähert.
-
Die Bahnebene a des Kometen ist durch das Zentrum
S und die Bahntangente t festgelegt.
-
Die Bahnparabel k ist durch Angabe des Brennpunkts S und des Linienelements
(K,t) eindeutig bestimmt: Spiegelt man die Gerade SF an der Tangente t
(in der Ebene a ), so erhält man einen
Parabeldurchmesser.
-
Der kürzeste Abstand Komet-Sonne ist der Abstand Parabelscheitel-Sonne;
die dazugehörige Kometenposition heißt Perihel bzw. Perigäum.
Zur konstruktiven Lösung des Beispiels sind folgende Grundoperationen
notwendig:
-
Hauptgeraden einer Ebene (Bestimmung von t")
-
Paralleldrehung einer allgemeinen Ebene (a in
1. Hauptlage drehen)
-
Scheinwerfereigenschaft einer Parabel (in parallelgedrehter Lage)
-
Krümmungskreis einer Parabel
-
Parabelkonstruktion aus 2 Linienelementen (Grundrißparabel)
-
Affin invariante Konstruktion von Parabelpunkten und Tangenten
Vorschläge
für einen projektartigen Unterrichtsablauf
Beide Themengebiete können in folgenden Schritten projektartig
erarbeitet werden:
-
Erarbeiten des Basiswissens in Gruppen: Es bilden sich mehrere Gruppen,
die jeweils eines der folgenden Themen behandeln: Geschichtliche Entwicklung
Physikalisches Modell Mathematische Herleitung Anwendungen der Kenntnisse
in benachbarten Sparten Die Gruppen sollen die notwendigen Informationen
durch ihre DG-, PH- und GSK-Lehrer, aus ihren Schulunterlagen (PH, GSK,
MA, ...) sowie aus Fachbüchern und Zeitschriften der Schulbibliothek,
... und der im Literaturverzeichnis angegebenen Werke erlangen.
-
Erweitern des Basiswissens durch Teamteaching (Physiklehrer !).
-
Präsentation des Basiswissens innerhalb der Klasse: Jedes Team stellt
seine Erkenntnisse in Form eines Kurzreferats dar. (Unterlagen kopieren
und an alle Gruppen verteilen.)
-
Lösen des Konstruktionsbeispiels: Das jeweilige Beispiel kann in gemeinsamen
Ge spräch mit dem Lehrer erarbeitet und eine Kon struktionsbeschreibung
angegeben werden.
-
Praktische Versuche und Demonstrationen: Wurfparabel: Experimentelle Kontrolle
der Rechenergebnisse im Beispiel Basketball 1 (Leibesübungen), Analyse
einer Stroboskobaufnahme (Physik), ... Planetenbewegung: Beobachtung einer
Planetenbahn, Aufnahme einer Planetenbahn mit großer Belichtungszeit
(mehrere Wochen!), Exkursion in Observatori en, ..
-
Festigung der Konstruktion durch ein HÜ-Beispiel: Die beigelegten
„Parallel"beispiele können als Hausübung aufgegeben werden.
-
Visualisierung mit Software: Zur Visualisierung können die beliegenden
Programme sowie mit Algebraprogramme (Derive, MathCad,..) erstellte Anwendungen
(siehe [4]) verwendet werden. Diese können durchaus
auch von Schülern erstellt werden.
-
Gestaltung eines Posters zur Präsentation außerhalb der Klasse:
Alle gesammelten Erkenntnisse und Unterlagen werden neu zusammengefaßt
und in einem Poster arrangiert. (Screenshots der Software!)
Literatur
[1] Dönhoff, H.: Selbst untersuchen
(Computer und Unterricht, 13/1994)
Dieser Artikel zeigt eine Möglichkeit, das Phänomen
Wurfparabel PC-gestützt und durch Schülerversuche zu besprechen.
Daneben befaßt sich der Autor mit der Frage, inwiefern der Einsatz
neuer Technologien im Unterricht ertragreich sein kann.
[2] Hund, F.: Geschichte der physikalischen
Begriffe (BI-Hochschul-Tb, 1968)
Diese Buch liefert einen Überblick über
die Entwicklung der Physik. Insbesondere versucht der Autor, den Wandel
in der Denkweise der Physiker und die damit verbundenen Änderungen
in der Bedeutung physikalischer Begriffe zu vermitteln. Dadurch gelingt
es, einen Einblick in die Kultur hinter der Physik darzubieten. Dieses
Buch ist leicht lesbar und zur Erweiterung des geschichtlichen Wissens
daher recht empfehlenswert.
[3] Jung, W.: Weltbild Kolleg Physik (Fischer
Tb, 1983)
In diesem Taschenbuch wird die Mittelschulphysik neu
aufbereitet präsentiert. Aufgrund des Umfangs und der damit verbundenen
Kompaktheit der Ausführungen ist das Buch zum Selbst studium nur bedingt
zu empfehlen.
[4] Keil, A.: Trainigsprogramm für Kugelstoßer
(MU 2/1997)
In diesem Artikel wird die mathematische Behandlung
der Wurfparabel sowie die Verwendung und die Visualisierung mit Algebraprogramm
Derive geschildert. Die beschriebene Vorgangsweise erscheint mir sehr praxisnahe,
der Beitrag daher sehr empfehlenswert.
[5] Paulsen, H.: Geometrieanteile im Physikunterricht
an AHS (Diplomarbeit, 1996)
Die unter der Anleitung von Prof. Dr. Weiß verfasste
Diplomarbeit behandelt Phänomene aus den Bereichen Raum-Zeit-Diagramme,
ebene Statik, Schwerpunkt, Wurfparabel und Planeten bewegung, Reflexion,
Brechung und Totalreflexion, Geometrie der Konstaktlinse und die spe zielle
Relativitätstheorie. Die Aufbereitung der Themen ist teils schuladäquat,
teils deutlich hochschulorientiert.
[6] Sexl u.a.: Physik 1und 2 (Hölder-Pichler-Tempsky,
1992)
[7] Schreiner, J.: Physik 1 und 2 (Hölder-Pichler-Tempsky,
1976)
[8] Apogee: Sharewareprogramm Bash1
In diesem Programm kommt die Wurfparabel als spielgestaltendes
Element ständig vor.
 Da es kaum
möglich ist, alle die Wurfbahn beeinflussenden Parameter in eine möglichst
einfache Universalformel einzubringen, treffen wir einige Vereinfachungen
(Idealisierungen):
Da es kaum
möglich ist, alle die Wurfbahn beeinflussenden Parameter in eine möglichst
einfache Universalformel einzubringen, treffen wir einige Vereinfachungen
(Idealisierungen):

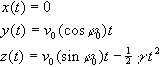 .
.![]()
![]() .
.![]() (in einem räumlichen Koordinatensystem mit Einheitsvektoren
(in einem räumlichen Koordinatensystem mit Einheitsvektoren ![]() ),
welches während des Wurfs durch die Schwerkraft beschleunigt wird.
Nach dem 2. Newtonsche Gesetz „Kraft
),
welches während des Wurfs durch die Schwerkraft beschleunigt wird.
Nach dem 2. Newtonsche Gesetz „Kraft ![]() =Masse
m · Beschleunigung
=Masse
m · Beschleunigung ![]() "
wirkt auf das Teilchen die Kraft
"
wirkt auf das Teilchen die Kraft
![]() .
.![]() .
.![]() ,
,![]() einen konstanten
Vektor (Integrationskonstante) darstellt. Unter Verwendung der Startwerte
j0
und v0 und der daraus resultierenden Startbedingung
einen konstanten
Vektor (Integrationskonstante) darstellt. Unter Verwendung der Startwerte
j0
und v0 und der daraus resultierenden Startbedingung
![]()
![]() .
Wir integrieren
.
Wir integrieren
![]()
![]() .
.![]() handelt es sich
um eine Schiebkonstante. Berücksichtigen wir die Starthöhe h0,
so erhalten wir die ausführlich geschriebene Parameterdarstellung
handelt es sich
um eine Schiebkonstante. Berücksichtigen wir die Starthöhe h0,
so erhalten wir die ausführlich geschriebene Parameterdarstellung
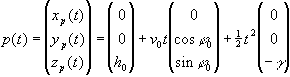 .
.![]() .
.![]()
![]() .
.

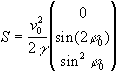 .
.

![]() ;
die Konstante k ist Produkt der Konstanten G
, p und q. Wir substituieren r=1/u und setzen f(1/u) in die Bewegungsgleichung
ein. Die entstehende Differentialgleichung
;
die Konstante k ist Produkt der Konstanten G
, p und q. Wir substituieren r=1/u und setzen f(1/u) in die Bewegungsgleichung
ein. Die entstehende Differentialgleichung
![]()
![]()
![]()
![]()
![]()
![]() .
.