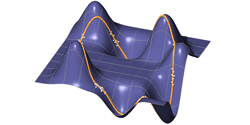

Abstract:
When designing curves on surfaces the need arises to approximate a given noisy target shape by a smooth fitting shape. We discuss the problem of fitting a B-spline curve to a point cloud by squared distance minimization in the case that both, the point cloud and the fitting curve, are constrained to lie on a smooth manifold. The on-manifold constraint is included by using the first fundamental form of the surface for squared distance computations between the point cloud and the fitting curve. For the solution we employ a constrained optimization algorithm that allows us to include further constraints such as one-sided fitting or surface regions that have to be avoided by the fitting curve. We illustrate the effectiveness of our algorithm at hand of several examples showing different applications.
Bibtex:
@article{floery-2007-ccfm,
author = "Simon Fl{\"o}ry and Michael Hofer",
title = "Constrained curve fitting on manifolds",
journal = "Computer-Aided Design",
volume = "40",
number = "1",
pages = "25-34",
year= "2008",
}
|
|