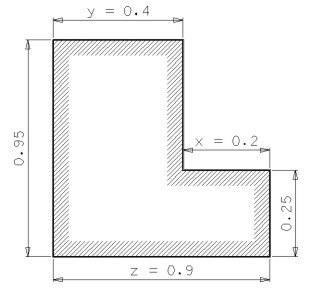
Bemerkung: Zur einfacheren Ausführung der Zeichnung werden eher unrealistische Meßwerte angenommen; die Schüler sollen das Prinzip der Ausgleichsrechnung und damit zusammenhängende Probleme erkennen.
In manchen Unterrichtssequenzen kann es vorkommen, daß gegebene
Angaben eines Objekts dieses überbestimmen; so kann es bereits in
der 3.Klasse Mathematik passieren, daß beim Abmessen der Dimensionen
eines Raumes (vgl. Beispiel 1) gewisse Maße einander widersprechen:

Bemerkung: Zur einfacheren Ausführung der Zeichnung werden
eher unrealistische Meßwerte angenommen; die Schüler sollen
das Prinzip der Ausgleichsrechnung und damit zusammenhängende Probleme
erkennen.
Unter der Voraussetzung, daß sämtliche Seitenwände des Wohnraumes normal zueinander stehen, gab es offensichtlich beim Bestimmen der „horizontalen" Dimensionen Meßungenauigkeiten, da 0,4 + 0,2 = 0,6 < 0,9 gilt.
Wie sollen die Werte für x, y und z nun tatsächlich gewählt werden, so daß die auftretenden Meßfehler möglichst gering sind, und was bedeutet „möglichst geringe Meßfehler"?
Bemerkung: In der Praxis sollte man, um Beobachtungs- bzw. Meßfehler möglichst auszugleichen, Messungen mehrfach und von verschiedenen Personen mit verschiedenen Meßgeräten ausführen lassen.
Zur Beantwortung der offenen Fragen, fassen wir die drei gemessenen Resultate vorerst mathematisch als lineares Gleichungssystem in den Variablen x und y (vgl. Arbeitsblatt 1).
So erhalten wir mit
| x = 0,4
y = 0,2 x + y = 0,9 |
(2.1)
|
ein überbestimmtes lineares Gleichungssystem, welches nur für exakt gemessene Werte lösbar ist. Da keine exakten Messungen vorliegen, dürfen wir aber auch nicht erwarten, daß die gesuchten Größen x und y die Gleichungen (2.1) erfüllen.
Bezeichnen wir nun die bei den drei Meßvorgängen auftretenden
Meßfehler mit ![]() ,
, ![]() und
und ![]() und
berücksichtigen wir diese in unserem Ansatz, so erhalten wir das Gleichungssystem
(2.2)
und
berücksichtigen wir diese in unserem Ansatz, so erhalten wir das Gleichungssystem
(2.2)
x - 0,4 = ![]()
y - 0,2 = ![]()
x + y - 0,9 = ![]()
Bemerkung: Die Gleichungen (2.2) werden als Fehlergleichungen,
die Größen ![]() als
Residuen
bezeichnet.
als
Residuen
bezeichnet.
Im Gleichungssystem (2.2)
sind die zu den exakten Größen x und y gehörigen
Residuen ![]() nicht
bekannt; wir wissen nur, daß das System nicht mit
nicht
bekannt; wir wissen nur, daß das System nicht mit ![]() =
= ![]() =
= ![]() = 0 erfüllbar ist. Eine sinnvolle Aufgabenstellung ist es nun, zu
fragen, ob es zwei Zahlen
= 0 erfüllbar ist. Eine sinnvolle Aufgabenstellung ist es nun, zu
fragen, ob es zwei Zahlen ![]() und
und ![]() gibt,
die eingesetzt in die Fehlergleichungen (2.2) Residuen ergeben, die
minimal
sind. Wobei wir noch nicht festgelegt haben, was minimal in diesem Zusammenhang
bedeuten soll.
gibt,
die eingesetzt in die Fehlergleichungen (2.2) Residuen ergeben, die
minimal
sind. Wobei wir noch nicht festgelegt haben, was minimal in diesem Zusammenhang
bedeuten soll.
Folgende Festlegungen für minimale Residuen wären denkbar (und führen auf mathematisch sinnvolle Fragestellungen):
Wir wollen mit der Fragestellung 3) beginnen, da dies auf ein einfach durchführbares, und daher gebräuchliches Rechenverfahren (Methode von GAUSS: Summe der kleinsten Fehlerquadrate) führt:
Bemerkung: Der geometrische Zugang ermöglicht uns auch die Lösung der beiden anderen Aufgaben, deren rechnerische Durchführung im allgemeinen doch eher kompliziert ist.
Mit den Vektoren a = (1/0/1), b = (0/1/1), c =
(0,4/0,2/0,9) und r = (![]() /
/![]() /
/![]() )
kann das Gleichungssystem (2.2) in der einfacheren (vektoriellen) Form
)
kann das Gleichungssystem (2.2) in der einfacheren (vektoriellen) Form
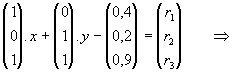 |
a.x + b.y - c = r |
(2.3)
|
geschrieben werden, wobei c als Konstantenvektor und r als Residuenvektor bezeichnet wird.
Die Gleichung (2.3) läßt nun eine einfache geometrische Interpretation zu:
Der Residuenvektor r kann als Differenz eines Vektors d = a.x + b.y und des Konstantenvektors c aufgefaßt werden, wobei der Vektor d als Linearkombination der Vektoren a und b geschrieben werden kann. Machen wir die Vektoren im Ursprung fest, so liegt der Vektor d in der von a und b aufgespannten Ebene.
Skizzieren wir diese Situation auf:
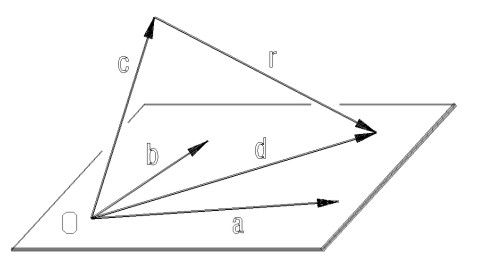 |
Nun ist es aber geometrisch naheliegend, diejenige Lösung als optimale Lösung unseres Problems anzusehen, für die der Residuenvektor r minimale Länge hat. Die (euklidische) Länge des Vektors r ist aber genau dann minimal, wenn der Vektor r zu der von a und b aufgespannten Ebene normal steht.
3) Erste geometrische Lösung (Arbeitsblatt 2)
Wir haben damit die in der Ebene gegebene Aufgabe (durch „räumliche Deutung") übergeführt in das darstellend geometrische Problem „Normale aus einem Punkt C auf eine Ebene OAB (M3), Durchstoßpunkt L einer Geraden mit einer Ebene".
Wir wählen als Zeicheneinheit 10cm (U’(50/140); U’’(50/150), tragen die Punkte A(1/0/1), B(0/1/1) und C(0,2/0,4/0,9) ein, konstruieren die zu OAB normale Gerade n und bestimmen den Durchstoßpunkt L von n mit der Ebene OAB.
Aus der Zeichnung können wir die Länge des Residuenvektors
r
(als
Maß für die Güte des Fehlerausgleichs) und den gesuchten
Lösungsvektor d ablesen. Auf Grund der speziellen Werte können
im Grundriß die Koordinaten x und y des Vektors d bezüglich
der Basisvektoren a und b (hier orthogonal und gleich lang)
abgemessen werden, womit die Lösung unseres Problems mit ![]() =
0,3 und
=
0,3 und ![]() =
0,5 vorliegt.
=
0,5 vorliegt.
Im Sinne der Methode der kleinsten Summe der Abstandsquadrate ist diese
Lösung optimal, da die (euklidische) Länge von r = ![]() nach dem Satz von Pythagoras und damit auch der Wert (
nach dem Satz von Pythagoras und damit auch der Wert (![]() ²
+
²
+ ![]() ²
+
²
+ ![]() ²)
minimal ist.
²)
minimal ist.
Bevor wir die beiden anderen Lösungsansätze (für minimale Residuen) angehen, wollen wir obiges Beispiel auch noch rechnerisch lösen.
Ein möglicher Weg zur Berechnung der Werte ![]() und
und ![]() besteht
darin, den Konstruktionsgang (Schnitt einer Geraden mit einer Ebene, Messen
von Koordinaten bezüglich einer Basis) nachzurechnen. Ein wenig eleganter
ist folgender Ansatz:
besteht
darin, den Konstruktionsgang (Schnitt einer Geraden mit einer Ebene, Messen
von Koordinaten bezüglich einer Basis) nachzurechnen. Ein wenig eleganter
ist folgender Ansatz:
r steht zur von a und b aufgespannten Ebene genau dann normal, wenn gilt:
r normal a, also r.a = 0 (skalares Produkt)
r normal b, also r.b = 0 (skalares Produkt)
Wenden wir diese Idee auf unsere Aufgabe an,
|
0 = r.a =
|
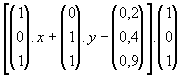 |
bzw. 0 = r.b =
|
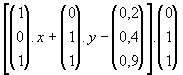 |
(4.1)
|
so erhalten wir das folgende lineare Gleichungssystem in den Variablen
x
und y:
|
(4.2)
|
woraus wir mit dem Gauss’schen Eliminationsverfahren rasch die Lösungen ![]() = 0,3 und
= 0,3 und ![]() =
0,5 finden.
=
0,5 finden.
Bevor wir weitere Interpretationen für minimale Residuen bearbeiten, wollen wir das Gelernte auf verschiedene Aufgabengebiete anwenden:
Bestimme eine lineare Funktion so, daß die Summe der Fehlerquadrate in y-Richtung minimal wird (Ausgleichsproblem bei Meßreihen).
|
x
|
|
|
|
|
f(x)
|
|
|
|
2)![]() (1 /1),
(1 /1), ![]() (2/2),
(2/2), ![]() (3/2)
(3/2)
6) Lösungsansätze für die Aufgaben
a) Mit Hilfe der Fehlergleichungen
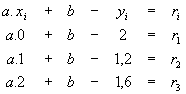 |
|
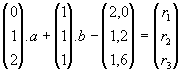 |
(6.1)
|
finden wir die Vektoren f = (0/1/2) (bestehend aus allen x-Werten
der Angabepunkte),
e = (1/1/1), c = (2,0/1,2/1,5) (bestehend aus den y-Werten
der Angabepunkte) und den gesuchten minimalen Residuenvektor r.
Die graphische Durchführung (Zeicheneinheit 5cm) und die rechnerische
Lösung führen beide auf die Gerade g: y = -0,2x
+ 1,8.
Wir haben in den vorigen Abschnitten die vorhandenen Meßfehler insofern korrigiert, daß die Summe der Quadrate der auftretenden Fehler minimal wird. Nun wollen wir diese Meßfehler nach anderen Methoden minimieren:
7) Methode des kleinsten maximalen Fehlers
In unserem Beispiel wollen wir nun Werte für die Längen x
und y ermitteln, so daß der größte auftretende
Meßfehler minimal wird. Geometrisch interpretiert bedeutet dies,
jenen Punkt L der Ebene OAB zu finden, für den gilt: der Betrag der
größten auftretenden Koordinatendifferenz ![]() ,
, ![]() und
und ![]() muß
minimal sein.
muß
minimal sein.
Bemerkung: Mathematisch gesehen führt uns dies auf die Fragestellung,
wann der Residuenvektur r im Sinne der Maximumnorm || x || :=
max(|![]() |,
|
|,
|![]() |, |
|, |![]() |)
minimal wird; dies wäre die Ausgleichung nach TSCHEBYSCHEFF.
|)
minimal wird; dies wäre die Ausgleichung nach TSCHEBYSCHEFF.
Bevor wir die Aufgabe im Raum lösen, überlegen wir uns die analoge Situation in der Ebene:
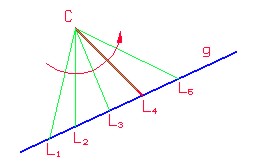
Unter den Vektoren ![]() suchen wir jenen heraus, für den die größte auftretende
Koordinatendifferenz
suchen wir jenen heraus, für den die größte auftretende
Koordinatendifferenz ![]() ,
, ![]() am kleinsten wird. Dies ist offensichtlich für jene Vektoren der Fall,
die die Richtungen (1/1) oder (1/-1) aufweisen.
am kleinsten wird. Dies ist offensichtlich für jene Vektoren der Fall,
die die Richtungen (1/1) oder (1/-1) aufweisen.
Übertragen wir unsere Erkenntnis in den Raum, so haben wir die Ebene OAB mit den durch C verlaufenden Geraden mit Richtungsvektoren (1/1/1), (1/-1/1), (1/1/-1) und (1/-1/-1) zu schneiden und den kürzesten Vektor OL zu finden („Durchstoßpunkt einer Geraden mit einer Ebene, Bestimmen der Länge einer Strecke (M1)".
Als Zeicheneinheit wählen wir wieder 10cm und konstruieren die
Durchstoßpunkte ![]() der vier Geraden
der vier Geraden ![]() durch C mit der Ebene OAB (Arbeitsblatt 3).
durch C mit der Ebene OAB (Arbeitsblatt 3).
Ein Schnittpunkt ![]() (-0,1/0,7/0,6)
tritt mit negativer x-Koordinate auf; dieser fällt als mögliche
Lösung aus.
(-0,1/0,7/0,6)
tritt mit negativer x-Koordinate auf; dieser fällt als mögliche
Lösung aus.
Die Punkte ![]() (0,5/0,7/1,2)
und
(0,5/0,7/1,2)
und ![]() (0,5/0,1/0,6)
führen auf Lösungen, bei denen der Betrag des Maximums der Meßfehler
jeweils 0,3 beträgt.
(0,5/0,1/0,6)
führen auf Lösungen, bei denen der Betrag des Maximums der Meßfehler
jeweils 0,3 beträgt.
Der Punkt ![]() (0,3/0,5/0,8)
führt zu einem maximalen Meßfehler von 0,1 und liefert die gesuchten
Lösungen
(0,3/0,5/0,8)
führt zu einem maximalen Meßfehler von 0,1 und liefert die gesuchten
Lösungen ![]() = 0,3 und
= 0,3 und ![]() = 0,5..
= 0,5..
Bemerkung: Für Ausgleichsrechnungen der vorgestellten Art sind die Lösungen für die euklidische und die Maximumsnorm immer gleich, da die Normale n zu Ebene OAB immer die Richtung (1/1/-1) aufweist; erst bei anderen Anwendungen treten unterschiedliche Ergebnisse auf.
Zur numerischen Lösung der Ausgleichung nach TSCHEBYSCHEFF rechnen wir am besten den Konstruktionsgang nach:
Wir berechnen die Durchstoßpunkte ![]() der
Geraden
der
Geraden ![]() ,
bestimmen anschließend die Koordinatendifferenzen der Vektoren
,
bestimmen anschließend die Koordinatendifferenzen der Vektoren ![]() und wählen als Lösung jenen Vektor r, für den das
Maximum dieser Differenzen am kleinsten ist. Werden die Werte
und wählen als Lösung jenen Vektor r, für den das
Maximum dieser Differenzen am kleinsten ist. Werden die Werte ![]() dieses Residuenvektors in (1.2) eingesetzt, so ergeben sich die gesuchten
Werte
dieses Residuenvektors in (1.2) eingesetzt, so ergeben sich die gesuchten
Werte ![]() =
0,3 und
=
0,3 und ![]() = 0,5.
= 0,5.
8) Methode der kleinsten Meßfehlersumme
Wir werden nun noch Werte für die Längen x und y
so ermitteln, daß die Summe der Beträge der auftretenden Meßfehler
minimal wird. Wir wollen dies wieder geometrisch interpretieren: Es gilt
jenen Punkt L der Ebene OAB zu finden, für den
|
(1.7)
|
minimal wird.
Wiederum betrachten wir die analoge Situation in der Ebene und suchen
jenen Vektor ![]() mit
der Eigenschaft
mit
der Eigenschaft ![]() +
+ ![]() ist
minimal. Wir erkennen, daß wir die Lösungen unter jenen Vektoren
suchen müssen, deren Richtungen parallel zu den Koordinatenachsen
verlaufen.
ist
minimal. Wir erkennen, daß wir die Lösungen unter jenen Vektoren
suchen müssen, deren Richtungen parallel zu den Koordinatenachsen
verlaufen.
Ebenfalls in der Zeicheneinheit 10cm lösen wir nun auch noch diese Aufgabe zu denselben Angabeelemente (Arbeitsblatt 4):
Im Raum müssen wir die Ebene OAB mit den durch C verlaufenden achsenparallelen
Geraden schneiden und den kürzesten Vektor ![]() bestimmen („Durchstoßpunkt einer projizerenden
Geraden mit einer Ebene - Angittern").
bestimmen („Durchstoßpunkt einer projizerenden
Geraden mit einer Ebene - Angittern").
9) Ein tieferer Einblick in die Materie
a) Normen und Einheitssphären:
Vom mathematischen Standpunkt aus handelt es sich bei allen drei Lösungsansätzen um das gleiche Problem, nämlich den kürzesten Vektor im Sinne einer gewissen Norm zu finden.
Bemerkung: Die verwendeten Normen, die Euklidische Norm (GAUSS),
die Maximumsnorm (TSCHEBYSCHEFF) und die ![]() -Norm
erfüllen alle folgende Eigenschaften:
-Norm
erfüllen alle folgende Eigenschaften:
1) Für jeden Vektor v gilt : || v || ![]() 0, falls || v || = 0
0, falls || v || = 0 ![]() v
= o
v
= o
2) Für jeden Vektor v gilt : || a.v || =| a | .|| v ||
3) || x + y || ![]() ||
x || + || y || (Dreiecksungleichung),
||
x || + || y || (Dreiecksungleichung),
was auch mit elementaren mathematischen Mitteln leicht nachvollziehbar ist.
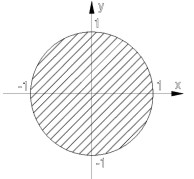
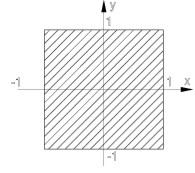
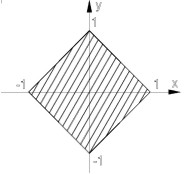
Um ein gewisses Gefühl für die drei verwendeten Normen zu erhalten und unsere geometrischen Konstruktionen aus einem anderen Blickwinkel zu sehen, betrachten wir die „Einheitsscheibe" in der Ebene
{x![]() R² mit ||
x
||
R² mit ||
x
|| ![]() 1}
1}![]()
bzw. den „Einheitsball" im Raum
{x![]() R³ mit ||
x
||
R³ mit ||
x
|| ![]() 1}.
1}.
Für die einzelnen Normen ergibt dies folgende Strukturen:
|
|
|
|
|
 |
 |
 |
|
|
|
|
|
|
| im R² |
|
|
|
| im R³ |
|
|
|
b) Messen mittels Einheitssphären:
Eine geometrische Interpretation der Abstandsbestimmung zwischen zwei Punkten A und B besteht nun darin, den Einheitskreis mit Mitte A so lange aufzublasen (zentrische Ähnlichkeit) bis der Punkt B auf der Oberfläche (Umfang) des Einheitskreises zu liegen kommt. Der Radius des so erhaltenen Einheitskreises ist die Länge der gesuchten Strecke (im Sinne der verwendeten Metrik).
Zur Bestimmung des Abstandes eines Punktes C von einer Ebene OAB müssen wir also die Einheitssphäre um den Mittelpunkt C so lange „aufblasen", bis diese die Ebene in einem Punkt L berührt. Die Gerade CL trägt dann den minimalen Abstand zwischen der Ebene und dem Punkt.
Bei der Verwendung der euklidischen Norm liegt der Berührpunkt L der Meßsphäre im (euklidischen) Normalfußpunkt; es gibt immer eine eindeutige Lösung.
Liegt die Maximumsnorm oder die L_1-Norm der Messung zugrunde, so können auch mehr als eine Lösung auftreten:
die Ebene ist zu einer Seitenfläche der Einheitssphäre parallel ---> zweiparametrige Schar von Lösungen
Im DG-Unterricht können wir nur die dreidimensionalen Aufgaben, also die Lösung der Ausgleichsrechnung für drei (voneinander abhängige) Messungen konstruktiv ausführen. Allgemein kann das Problem für n mit Fehlern behafteten Messungen die Ausgleichsrechnung durchzuführen auf die Bestimmung des kürzesten Abstandes zwischen einem Punkt C und einer Hyperebene zurückgeführt werden.
[1] Nipp K., Stoffer D. „Lineare Algebra", Verlag der Fachvereine Zürich, 1992, Zürich
Solides Lehrbuch mit etlichen Übungsaufgaben; besonders numerische Aspekte der linearen Algebra werden berücksichtigt.
[2] Wolf U. „Konstruktion der Ausgleichsgeraden dreier Punkte", Der Mathematikunterricht 2/82, S. 57-65, Ernst Klett Verlag, Stuttgart
Ein Spezialfall für die Ausgleichsrechnung nach Gauss wird darstellend geometrisch behandelt.