|
Nonlinear Subdivision
Curve subdivision schemes on manifolds and in Lie groups are constructed from linear subdivision schemes by first representing the rules of affinely invariant linear schemes in terms of repeated affine averages, and then replacing the operation of affine average either by a geodesic average (in the Riemannian sense or in a certain Lie group sense), or by projection of the affine averages onto a surface. The analysis of these schemes is based on their proximity to the linear schemes which they are derived from.
|

|
Smoothness of Nonlinear Subdivision Process
Principal Investigator: Johannes Wallner
Austrian Science Fund (FWF) project P18575
(continued at Graz University of Technology)
|

|
J. Wallner and N. Dyn.
Convergence and C1 analysis of subdivision
schemes on manifolds by proximity.
Comput. Aided Geom. Design 22/7 (2005), 593-622.
We verify that a linear scheme S and its analogous nonlinear scheme T satisfy a proximity condition. We further show that the proximity condition implies the convergence of T and continuity of its limit curves, if S has the same property, and if the distances of consecutive points of the initial control polygon are small enough. Moreover, if S satisfies a smoothness condition which is sufficient for its limit curves to be C1, and if T is convergent, then the curves generated by T are also C1.
|
|
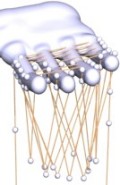
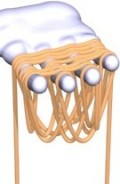
J. Wallner and H. Pottmann.
Intrinsic
subdivision with smooth limits for graphics and animation.
ACM Trans. Graphics 25/2 (2006), 356-374.
This paper shows the capabilities of intrinsic curve subdivision in nonlinear geometries (like a surface, the group of Euclidean motions, or Euclidean space minus obstacles). A wide class of perturbations of linear schemes and many intuitive ways of placing control points/positions lead to smooth freeform curves/motions. We discuss geodesic subdivision, curves on level sets, obstacles, modelling of kinematic surfaces, interactive design of smooth motions with gliding and obstacle side conditions, and multibody kinematic chains.
Apart from the nonlinearities entailed by the underlaying geometry, subdivision schemes are perturbed by discretisation and incomplete computing. Even with such errors present we can stay within the realm of smooth limits.
|
|
|
Publications
-
P. Grohs.
Smoothness analysis of subdivision schemes on regular grids by proximity.
Technical Report 166, Geometry Preprint Series, Vienna Univ. of Technology, September 2006.
-
J. Wallner, E. Nava Yazdani, and P. Grohs.
Smoothness
properties of Lie group subdivision schemes.
Technical Report 165, Geometry Preprint Series, Vienna Univ. of Technology,
November 2006.
-
J. Wallner and N. Dyn.
Convergence and C1 analysis of subdivision
schemes on manifolds by proximity.
Comput. Aided Geom. Design 22/7 (2005), 593-622.
[MR].
-
J. Wallner and H. Pottmann.
Intrinsic
subdivision with smooth limits for graphics and animation.
ACM Trans. Graphics 25/2 (2006), 356-374.
-
J. Wallner.
Smoothness
analysis of subdivision schemes by proximity.
Constr. Approx. 24/3 (2006), 289-318.
|
|
Quick Links
Johannes Wallner
Discrete Differential Geometry
Developable Surfaces
Geometric Spline Theory
Geometric Tolerancing
Sitemap
External Links

Austrian Science Fund (FWF)
|


