|
Welcome to the research group
Differential Geometry and Geometric Structures
|
|
Members & friends of the group in Jul 2021
photograph © by Narges Lali
|
Differential geometry has been a thriving area of research
for more than 200 years, employing methods from analysis
to investigate geometric problems. Typical questions
involve the shape of smooth curves and surfaces and the
geometry of manifolds and Lie groups. The field is at
the core of theoretical physics and plays an important
role in applications to engineering and design.
Finite and infinite geometric structures are ubiquitous
in mathematics. Their investigation is often intimately
related to other areas, such as algebra, combinatorics or
computer science.
These two aspects of geometric research stimulate and
inform each other, for example, in the area of "discrete
differential geometry", which is particularly well suited
for computer aided shape design.
|
|
Gallery of some research interests and projects
Symmetry breaking in geometry:
We discuss a geometric mechanism that may,
in analogy to similar notions in physics,
be considered as "symmetry breaking" in geometry.
(Fuchs, Hertrich-Jeromin, Pember;
Fig ©Nimmervoll)
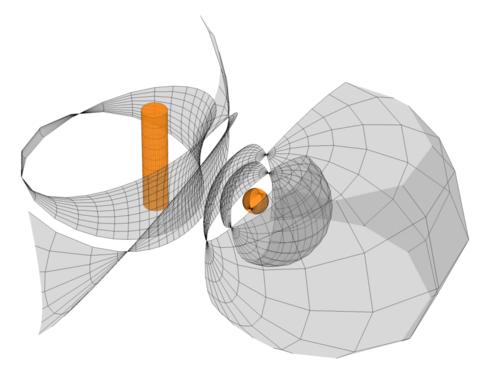
Cyclic coordinate systems:
an integrable discretization in terms of a discrete flat
connection is discussed.
Examples include systems with discrete flat fronts or
with Dupin cyclides as coordinate surfaces
(Hertrich-Jeromin, Szewieczek)
We study surfaces with a family of
spherical curvature lines
by evolving an initial spherical curve through
Lie sphere transformations,
e.g., the Wente torus
(Cho, Pember, Szewieczek)
Discrete Weierstrass-type representations
are known for a wide variety of discrete surfaces classes.
In this project, we describe them in a unified manner,
in terms of the Omega-dual transformation applied to
to a prescribed Gauss map.
(Pember, Polly, Yasumoto)
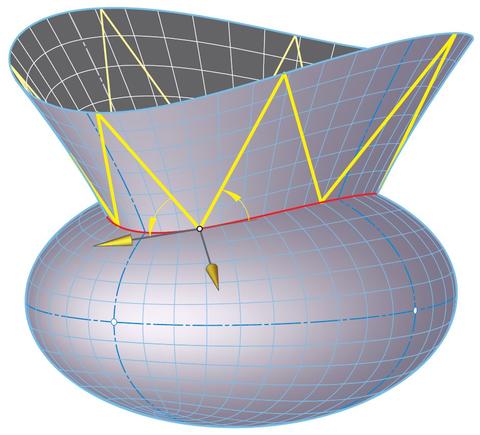
Billiards:
The research addresses invariants of trajectories of a
mass point in an ellipse with ideal physical reflections
in the boundary. Henrici's flexible hyperboloid paves the
way to transitions between isometric billiards in ellipses
and ellipsoids (Stachel).
Spreads and Parallelisms:
The topic of our research are connections among spreads
and parallelisms of projective spaces with areas like
the geometry of field extensions, topological geometry,
kinematic spaces, translation planes or flocks of quadrics.
(Havlicek)
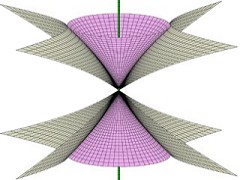
This is a surface of (hyperbolic) rotation in hyperbolic
space that has constant Gauss curvature,
a
recent classification project.
(Hertrich-Jeromin, Pember, Polly)
Geometric shape generation:
We aim to understand geometric methods to generate
and design (geometric) shapes,
e.g., shape generation by means of representation formulae,
by transformations, kinematic generation methods, etc.
(Hertrich-Jeromin, Fig Lara Miro)
Affine Differential Geometry:
In affine differential geometry a main point of research is
the investigation of special surfaces in three dimensional
affine space.
(Manhart)
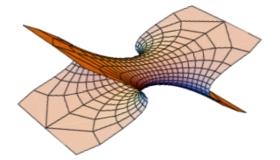
Transformations & Singularities:
We aim to understand how transformations of particular
surfaces behave (or fail to behave) at singularities, and
to study how those transformations create (or annihilate)
singularities.
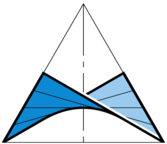
The figure shows the isothermic dual of an ellipsoid,
which is an affine image of a minimal
Scherk tower.
(Hertrich-Jeromin)
|
|
News
- 18 Jun 2026: Geometry seminar
- Eleni Pachyli (TU Wien): TBA
- 11 Jun 2026: Geometry seminar
- Ivan Izmestiev (TU Wien): Discrete Wirtinger inequality
Abstract
The classical Wirtinger inequality compares the $L_2$-norm of a
periodic function with zero average with the $L_2$-norm of its
derivative. It was used by Hurwitz to give a new proof of the
isoperimetric inequality for smooth curves. A discrete version
of the Wirtinger inequality is due to Fan, Taussky, and Todd. In
this talk a generalization of the Fan-Taussky-Todd inequality
will be stated and proved.
- 03 Jun 2026, 12:00 CEST: JA, surfaces and beyond
- Shintaro Akamine (Nihon University):
Constant mean curvature surfaces in the three-dimensional light cone
Abstract
Some classes of surfaces in spaces equipped with degenerate
metrics often arise in correspondence with minimal surfaces
in Euclidean space and maximal surfaces in Lorentz-Minkowski
space. In this talk, we present local and global properties
of spacelike constant mean curvature surfaces in the
three-dimensional light cone. In particular, we explain
Bernstein-type theorems for such surfaces. This talk is
based on the joint work with Wonjoo Lee (Jeonbuk National
University) and Seong-Deog Yang (Korea University).
- 28 May 2026: Geometry seminar
- Darius Imre (TU Wien):
Die Geometrie der Addition und Multiplikation
Abstract
In diesem Vortrag konstruieren wir, ausgehend von einer
Menge von Punkten, Geraden und einer Inzidenzrelation, die
zusammen eine projektive Ebene bilden, eine Addition und eine
Multiplikation. Dazu untersuchen wir einige Eigenschaften von
Homologien und Elationen und verwenden diese anschliessend zur
Konstruktion eines Schiefkörpers. Dabei werden wir sehen,
dass die Existenz der dafür benötigten Abbildungen nur in
desarguesschen Ebenen garantiert ist. Abschliessend betrachten
wir die erweiterte euklidische Ebene und zeigen, dass der
dort entstehende Schiefkörper isomorph zu
den reellen Zahlen ist.
- 21 May 2026: Geometry seminar
- Michal Zamboj (Charles University Prague):
Von Staudts synthetic constructions of algebraic operations on complex and split-complex numbers
Abstract
Over the years 1847-1856, in "Geometrie der Lage and Beiträge
zur Geometrie der Lage", Karl Georg Christian von Staudt
formalized projective geometry based on incidence properties. He
introduced synthetic constructions - on points and lines with
respect to a fixed conic - corresponding to operations on the
extended real numbers. We show a generalization of von
Staudt's constructions to the complex and split-complex
numbers via projection onto the Riemann sphere and subsequent
models on quadrics. Consequently, we present a geometric
algorithm for the synthetic construction of Gaussian primes on a
paraboloid of revolution.
- 07 May 2026: Geometry seminar
- Christopher Latour (TU Wien):
Elliptic Curves, Complex Tori and Moduli Spaces
Abstract
A projective nonsingular curve defined by a homogeneous
polynomial of degree 3 is called an elliptic curve. The study of
elliptic curves plays an integral part in modern mathematics and
is at the heart of many famous results, such as Fermats Last
Theorem. In this talk we will investigate the structure of
elliptic curves over $\mathbb{C}$ and their connection to
complex tori and elliptic functions. This connection will enable
us to represent the quotient space of all elliptic curves modulo
isomorphism as a Riemann surface, where every point of the
Riemann surface corresponds to an equivalence class of elliptic
curves. Such spaces are called moduli spaces and we will take a
look at further moduli spaces of elliptic curves.
- 06 May 2026, 12:00 CEST: JA, surfaces and beyond
- Katrin Leschke (University of Leicester):
Links between the integrable systems of a CMC surface
Abstract
A CMC surface in 3-space is constrained Willmore and
isothermic. It is well known that these 3 surface classes are
each determined by a family of flat connections. In this talk
we discuss links between the corresponding families of flat
connections: we show that parallel sections of the associated
family of flat connections of one family give algebraically
the parallel sections of the other families. In particular,
we obtain links between transformations of CMC surfaces,
isothermic surfaces and constrained Willmore surfaces which
are given by parallel sections, such as the associated family,
the simple factor dressing and the Darboux transformation.
- 16 Apr 2026: Geometry seminar
- Elizaveta Streltsova (IST Austria):
Face numbers of polytopes and levels in arrangements
Abstract
Levels in arrangements are a fundamental notion in discrete and
computational geometry and are a natural generalization of
convex polytopes. In the talk, I will present the relevant
background from convex polytope theory and two new results on
the face numbers of levels in arrangements. Collectively, these
numbers form the $f$-matrix (which generalizes the $f$-vector of a
polytope). We determine the affine space spanned by the
$f$-matrices of all arrangements of n hemispheres in $S^d$. This
completes a long line of research on linear relations between
face numbers and answers a question posed by Andrzejak and Welzl
in 2003. Moreover, we proved a special case $n = d + 4$ of the
long-standing conjecture of Eckhoff, Linhart, and Welzl on the
complexity of the ($\leq k$)-levels, which implies the Harary-Hill
Conjecture on the number of crossings of complete graphs for the
class of spherical arc drawings. For the proofs, we introduce
the $g$-matrix, which encodes the $f$-matrix and generalizes the
classical $g$-vector of a polytope.
Joint work with Uli Wagner.
- 05 Mar 2026: Geometry seminar
- Matthias Pichelbauer (TU Wien): Alpha-Shapes
Abstract
This talk presents an introduction to alpha shapes, a concept
that generalizes the notion of convex hulls. Based on the ideas
developed in the paper "On the Shape of a Set of Points in the
Plane" by Herbert Edelsbrunner, David G.Kirkpatrick and
Raimund Seidel, alpha shapes provide a flexible way to capture
the shape of a finite point set, controlled by a parameter that
allows for varying levels of detail.
The talk focuses primarily on the construction of alpha shapes
and highlights their close relationship with Delaunay
triangulations. In particular, it explains how alpha shapes can
be derived as subcomplexes of the Delaunay triangulation, making
this connection central to both their theoretical understanding
and practical computation.
|
Technische Universität Wien
