|
|
P28427-N35: Non-rigidity and Symmetry breaking
Research Project (FWF)
|
|

|
Project leader: Udo Hertrich-Jeromin
Funding period: 1 Oct 2016 - 31 Mar 2022
(approved 5 Oct 2015)
Field: Mathematics;
Areas: Differential geometry, Integrable systems
|
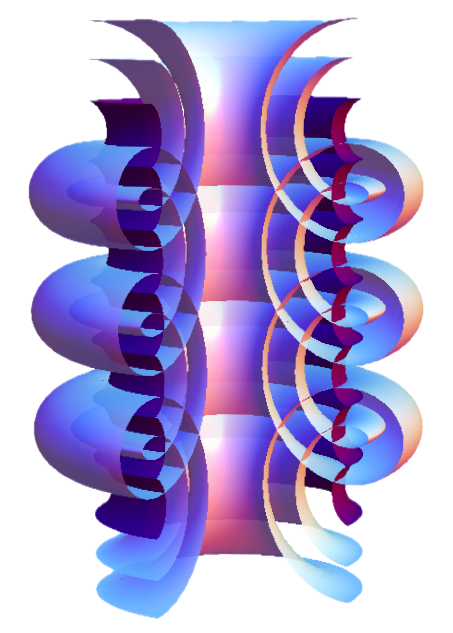 Channel linear Weingarten surfaces
Channel linear Weingarten surfaces
(Fig: K Mundilova)
|
Abstract.
Properties or equations used to
specify geometric objects possess certain symmetries, such as the
specification of a triangle in terms of three angles, which determines
a triangle up to similarity, or in terms of three edge lengths, which
determines it up to Euclidean motion: these two specifications have
different symmetry groups. Various theorems in geometry describe a
situation, whereby a "conserved quantity",
naturally associated with a geometric object, reduces the symmetry
group of its defining properties:
the original symmetry is broken.
Vessiot's theorem yields a classical example of symmetry breaking in
differential geometry: if a surface can be deformed while preserving
all properties relating to angle measurement and, at the same time,
envelops a 1-parameter family of spheres, then it is piece of a cone,
a cylinder or a surface of revolution. The first two properties only
depend on an angle measurement, while being a cone, cylinder or
surface of revolution depends on a length measurement.
Thus symmetry breaking has occurred.
We will investigate relations between non-rigidity and symmetry
breaking, in particular, whether deformability in more than one way
invariably leads to symmetry breaking, thus generalizing Vessiot's
theorem. However, our main concern will be to detect
causes for symmetry breaking
rather than just its occurrence, for example, by studying the
appearance of the aforementioned "conserved quantities".
|
|
Publications.
- M Pember, G Szewieczek (2018)
-
Channel surfaces in Lie sphere geometry;
Beitr Algebra Geom 59, 779-796 (2018)
DOI:10.1007/s13366-018-0394-6
Abstract
We discuss channel surfaces in the context of Lie
sphere geometry and characterise them as certain
$\Omega_0$-surfaces. Since $\Omega_0$-surfaces possess
a rich transformation theory, we study the behaviour of
channel surfaces under these transformations. Furthermore,
by using certain Dupin cyclide congruences, we characterise
Ribaucour pairs of channel surfaces.
- F Burstall, U Hertrich-Jeromin, M Pember, W Rossman (2019)
-
Polynomial conserved quantities of Lie applicable surfaces;
manuscripta math 158, 505-546 (2019)
DOI:10.1007/s00229-018-1033-0
Abstract
Using the gauge theoretic approach for Lie applicable
surfaces, we characterise certain subclasses of surfaces
in terms of polynomial conserved quantities. These include
isothermic and Guichard surfaces of conformal geometry and
L-isothermic surfaces of Laguerre geometry. In this setting
one can see that the well known transformations available
for these surfaces are induced by the transformations of
the underlying Lie applicable surfaces. We also consider
linear Weingarten surfaces in this setting and develop a
new Bäcklund-type transformation for these surfaces.
- M Pember, W Rossman, K Saji, K Teramoto (2019)
-
Characterizing singularities of a surface in Lie sphere geometry;
Hokkaido Math J 48(2), 281-308 (2019)
DOI:10.14492/hokmj/1562810509,
EPrint arXiv:1703.04257
Abstract
The conditions for a cuspidal edge, swallowtail and other
fundamental singularities are given in the context of Lie
sphere geometry. We then use these conditions to study the
Lie sphere transformations of a surface.
- M Pember (2020)
-
G-deformations of maps into projective space;
Boll Unione Mat Ital 13, 275-292 (2020)
DOI:10.1007/s40574-020-00218-9,
EPrint arXiv:1712.06945
Abstract
$G$-deformability of maps into projective space is characterised
by the existence of certain Lie algebra valued 1-forms. This
characterisation gives a unified way to obtain well known
results regarding deformability in different geometries.
- M Pember (2020)
-
Weierstrass-type representations;
Geom Dedicata 204, 299-309 (2020)
DOI:10.1007/s10711-019-00456-y
Abstract
Weierstrass-type representations have been used extensively
in surface theory to create surfaces with special curvature
properties. In this paper we give a unified description of
these representations in terms of classical transformation
theory of $\Omega$-surfaces.
- M Pember (2020)
-
Lie applicable surfaces;
Commun Anal Geom 28, 1407-1450 (2020)
DOI:10.4310/CAG.2020.v28.n6.a5,
EPrint arXiv:1606.07205
Abstract
We give a detailed account of the gauge-theoretic approach
to Lie applicable surfaces and the resulting transformation
theory. In particular, we show that this approach coincides
with the classical notion of $\Omega$- and $\Omega_0$-surfaces
of Demoulin.
- F Burstall, M Pember (2022)
-
Lie applicable surfaces and curved flats;
manuscripta math 168, 525-533 (2022)
DOI:10.1007/s00229-021-01304-8
Abstract
We investigate curved flats in Lie sphere geometry. We
show that in this setting curved flats are in one-to-one
correspondence with pairs of Demoulin families of Lie
applicable surfaces related by Darboux transformation.
- A Fuchs, U Hertrich-Jeromin, M Pember (2022)
-
Symmetry breaking in geometry;
EPrint arXiv:2206.13401
(2022)
Abstract
A geometric mechanism that may, in analogy to similar
notions in physics, be considered as "symmetry breaking"
in geometry is described, and several instances of this
mechanism in differential geometry are discussed: it is
shown how spontaneous symmetry breaking may occur, and it
is discussed how explicit symmetry breaking may be used
to tackle certain geometric problems. A systematic study
of symmetry breaking in geometry is proposed, and some
preliminary thoughts on further research are formulated.
- F Burstall, J Cho, U Hertrich-Jeromin, M Pember, W Rossman (2023)
-
Discrete $\Omega$-nets and Guichard nets via discrete Koenigs nets;
Proc London Math Soc 126(2), 790-836 (2023)
DOI:10.1112/plms.12499
Abstract
We provide a convincing discretisation of Demoulin's
$\Omega$-surfaces along with their specialisations to Guichard
and isothermic surfaces with no loss of integrable structure.
- J Cho, M Pember, G Szewieczek (2023)
-
Constrained elastic curves and surfaces with spherical curvature lines;
Indiana Univ Math J 72(5), 2059-2099 (2023)
DOI:10.1512/iumj.2023.72.9487,
EPrint arXiv:2104.11058
Abstract
In this paper, we consider surfaces with one or two families
of spherical curvature lines. We show that every surface
with a family of spherical curvature lines can locally be
generated by a pair of initial data: a suitable curve of
Lie sphere transformations and a spherical Legendre curve.
We the provide conditions on the initial data for which
such a surface is Lie applicable, an integrable class of of
surfaces that includes cmc and pseudospherical surfaces.
In particular, we show that a Lie applicable surface with
exactly one family of spherical curvature lines must be
generated by the lift of a constrained elastic curve in some
space form. In view of this goal, we give a Lie sphere
geometric characterisation of constrained elastic curves
via polynomial conserved quantities of a certain family
of connections.
- U Hertrich-Jeromin, M Pember, D Polly (2023)
-
Channel linear Weingarten surfaces in space forms;
Beitr Algebra Geom 64, 969-1009 (2023)
DOI:10.1007/s13366-022-00664-w,
EPrint arXiv:2105.00702
Abstract
Channel linear Weingarten surfaces in space forms are
investigated in a Lie sphere geometric setting, which allows
for a uniform treatment of different ambient geometries. We
show that any channel linear Weingarten surface in a space form
is isothermic and, in particular, a surface of revolution in
its ambient space form. We obtain explicit parametrisations for
channel surfaces of constant Gauss curvature in space forms,
and thereby for a large class of linear Weingarten surfaces
up to parallel transformation.
- M Pember, D Polly, M Yasumoto (2023)
-
Discrete Weierstrass-Type Representations;
Discrete Comput Geom 70, 816-844 (2023)
DOI:10.1007/s00454-022-00439-z,
EPrint arXiv:2105.06774
Abstract
Discrete Weierstrass-type representations yield a construction
method in discrete differential geometry for certain classes
of discrete surfaces. We show that the known discrete
Weierstrass-type representations of certain surface classes
can be viewed as applications of the $\Omega$-dual transform
to lightlike Gauss maps in Laguerre geometry. From this
construction, further Weierstrass-type representations
arise. As an application of the techniques we develop,
we show that all discrete linear Weingarten surfaces of
Bryant or Bianchi type locally arise via Weierstrass-type
representations from discrete holomorphic maps.
|
|
People
Birgit Slama (Secretary)
Andreas Fuchs
Udo Hertrich-Jeromin
Mason Pember
Denis Polly
Links
FWF
- Austrian Science Fund
TUW
- Vienna University of Technology
DMG
- Institute of Discrete Mathematics and Geometry
|

 Technische Universität Wien
Technische Universität Wien