Geometric Tolerancing

Geometric Set Operations for Tolerancing in CAD

Principal Investigator: Johannes Wallner
Austrian Science Fund (FWF) project P15911

M. Hofer, G. Sapiro, and J. Wallner. Fair polyline networks for constrained smoothing of digital terrain elevation data. IEEE Trans. Geosc. Remote Sensing 44/10/2 (2006), 2983-2990.

We present a framework which uses fair polyline networks for smoothing digital terrain elevation data with guaranteed error bounds and feature preservation. The algorithm is capable of smoothing the terrain data with tolerance cylinders of different sizes. These flexible tolerances have two advantages in particular: (i) we can preserve features present in the data by reducing the size of the tolerance cylinders in feature areas, (ii) the algorithm can be used to fill holes present in the original data during the smoothing process. Single contour lines are smoothed via processing of a small neighborhood of that contour line.

H.-P. Schröcker and J. Wallner: Curvatures and Tolerances in the Euclidean Motion Group. Results Math. 47 (2005), 132-146.

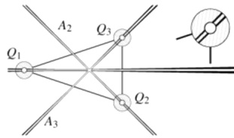
We investigate the action of imprecisely defined affine and Euclidean transformations and compute tolerance zones of points and subspaces. Tolerance zones in the Euclidean motion group are analysed by means of linearisation and bounding the linearisation error via the curvatures of that group with respect to an appropriate metric.

J. Wallner, H.-P. Schröcker, and S. Hu. Tolerances in geometric constraint problems. Reliab. Comput. 11, 234-251 (2005).

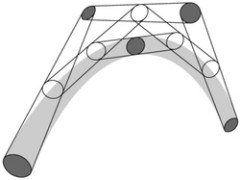
We study error propagation through implicit geometric problems by linearising and estimating the linearisation error. The method is particularly useful for quadratic constraints, which turns out to be no big restriction for many geometric problems in applications.

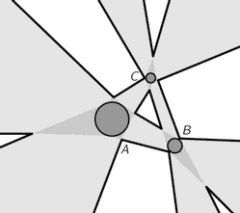
J. Wallner, R. Krasauskas,, H. Pottmann: Error Propagation in Geometric Constructions, Computer-Aided Design 32 (2000), 631-641.

In this paper we consider error propagation in geometric constructions from a geometric viewpoint. First we study affine combinations of convex bodies: This has numerous examples in spline curves and surfaces defined by control points. Second, we study in detail the circumcircle of three points in the Euclidean plane. It turns out that the right geometric setting for this problem is Laguerre geometry and the cyclographic mapping, which provides a point model for sets of circles or spheres.

H. Pottmann, B. Odehnal, M. Peternell, J. Wallner, R. Ait Haddou: On optimal tolerancing in Computer-Aided Design In: R. Martin and W. Wang, eds., Geometric Modeling and Processing 2000, IEEE Computer Society, Los Alamitos, CA, 2000, pp. 347-363.

A geometric approach to the computation of precise or well approximated tolerance zones for CAD constructions is given. We continue a previous study of linear constructions and freeform curve and surface schemes under the assumption of convex tolerance regions for points. The computation of the boundaries of the tolerance zones for curves and surfaces is discussed. We also study congruence transformations in the presence of errors and families of circles arising in metric constructions under the assumption of tolerances in the input. The classical cyclographic mapping as well as ideas from convexity and classical differential geometry appear as central geometric tools.