
A lecture on multilinear algebra in June 1998
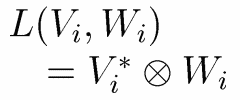
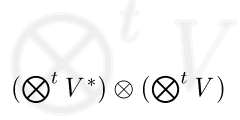

Rotation of a vector field
|
1. Tensor Products
- Multilinear mappings of vector spaces
- Existence and universal property of the tensor product
- Commutativity and associativity of the tensor product
- The tensor product in terms of coordinates
- Tensor products and spaces of linear mappings
- Kronecker product of linear mappings (matrices)
- Contraction
- Lowering and raising of indices
- Duality
2. Tensor Algebras
- Covariant, contravariant and mixed tensors
- Classical definition and notation of a tensor in terms of coordinates
- Structure tensor of an algebra
- Mixed tensor algebra
- Universal property of the tensor algebra
3. Exterior Algebras
- Exterior powers and p-vectors
- Grassmann coordinates of subspaces
- Alternation operator
- Exterior powers of linear mappings
- Exterior algebra
- Duality and p-forms
- Exterior algebra
- Decomposable p-vectors
4. Clifford Algebras
- Quadratic forms
- Clifford mappings
- Clifford mappings and exterior algebra
- Clifford Algebras
- Dimension of a Clifford algebra
- Examples of Clifford algebras
- Structures on a Clifford algebra
5. Spinors
- Clifford groups and spin groups
- Isometries
- The centre of a Clifford algebra
- Semisimple modules and representation of algebras
- Spaces of spinors
|

