We consider large boolean functions over  variables
variables 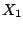 ,
,
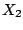 ,...,
,...,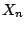 . Any such function can be represented (or computed)
by a complete binary tree with and or or in the internal
nodes and a literal in the external nodes. Many different trees can
represent the same function, so that a fundamental question is related
to the so-called ``complexity'' of a boolean function :
. Any such function can be represented (or computed)
by a complete binary tree with and or or in the internal
nodes and a literal in the external nodes. Many different trees can
represent the same function, so that a fundamental question is related
to the so-called ``complexity'' of a boolean function :
The existence of a
limiting probability distribution 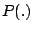 on the set of (finite or
infinite) and/or trees was shown by Lefmann and
Savicky [LS97]. We give here an alternative proof of the
existence of this distribution, which leads to effective computation
in simple cases. We also consider the relationship between the
probability
on the set of (finite or
infinite) and/or trees was shown by Lefmann and
Savicky [LS97]. We give here an alternative proof of the
existence of this distribution, which leads to effective computation
in simple cases. We also consider the relationship between the
probability 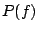 and the complexity
and the complexity 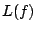 of a boolean
function
of a boolean
function 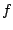 . The approach by Lefmann and Savicky leads to the
following inequalities :
. The approach by Lefmann and Savicky leads to the
following inequalities :
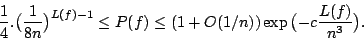 |
(1) |
A
detailed analysis of the functions enumerating some sub-families of
trees, and of their radius of convergence, allows us to improve the
upper bound, from
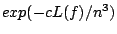 to
to
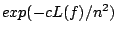 .
.
- LS97
-
Hanno Lefmann and Petr Savický.
Some typical properties of large AND/OR Boolean formulas.
Random Structures Algorithms, 10(3):337-351, 1997.
Back to the Index
Please send comments and corrections to Thomas Klausner.
![]() variables
variables ![]() ,
,
![]() ,...,
,...,![]() . Any such function can be represented (or computed)
by a complete binary tree with and or or in the internal
nodes and a literal in the external nodes. Many different trees can
represent the same function, so that a fundamental question is related
to the so-called ``complexity'' of a boolean function :
. Any such function can be represented (or computed)
by a complete binary tree with and or or in the internal
nodes and a literal in the external nodes. Many different trees can
represent the same function, so that a fundamental question is related
to the so-called ``complexity'' of a boolean function :