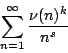
The asymptotic behaviour of the summatory function of several digital functions has been studied using Mellin-transform techniques in [FGK$^+$94]. There it remained open how to treat the higher moments of the sum-of-digits function and other digital functions using the same technique. The problem was that estimates for the corresponding Dirichlet series could not be found. We present estimates for the Dirichlet series
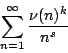
on the line ![]() which allow to prove convergence of the
integrals in the remainder term of the Mellin-Perron formula as well
as absolute convergence of the Fourier series of the periodic
fluctuations.
which allow to prove convergence of the
integrals in the remainder term of the Mellin-Perron formula as well
as absolute convergence of the Fourier series of the periodic
fluctuations.