It is known that the joint distribution of the number of nodes of each
type of a 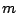 -ary search tree is multivariate normal when
-ary search tree is multivariate normal when 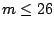 ([LM94], [CH01], [Hwa02]).
([LM94], [CH01], [Hwa02]).
When 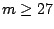 , we show the following strong (
, we show the following strong (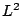 ) asymptotics of
the random vector
) asymptotics of
the random vector
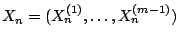 , where
, where
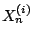 denotes the number of nodes containing
denotes the number of nodes containing 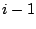 keys after
having introduced
keys after
having introduced 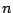 keys in the tree: there exists deterministic
vectors
keys in the tree: there exists deterministic
vectors 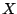 ,
, 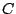 and
and 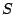 and random variables
and random variables 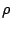 and
and 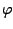 such that
such that
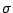 and
and 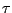 denote the real
and imaginary parts of one of the eigenvalues of the transition
matrix, having the second greatest real part.
denote the real
and imaginary parts of one of the eigenvalues of the transition
matrix, having the second greatest real part.
- CH01
-
Hua-Huai Chern and Hsien-Kuei Hwang.
Phase changes in random 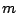 -ary search trees and generalized
quicksort.
-ary search trees and generalized
quicksort.
Random Structures Algorithms, 19(3-4):316-358, 2001.
Analysis of algorithms (Krynica Morska, 2000).
- Hwa02
-
Hsien-Kuei Hwang.
Second phase changes in random 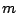 -ary search trees and generalized
quicksort: convergence rates.
-ary search trees and generalized
quicksort: convergence rates.
To appear in the Annals of Probability. Paper available at
http://algo.stat.sinica.edu.tw/, 2002.
- LM94
-
William Lew and Hosam M. Mahmoud.
The joint distribution of elastic buckets in multiway search trees.
SIAM J. Comput., 23(5):1050-1074, 1994.
Back to the Index
Please send comments and corrections to Thomas Klausner.
![]() -ary search tree is multivariate normal when
-ary search tree is multivariate normal when ![]() ([LM94], [CH01], [Hwa02]).
([LM94], [CH01], [Hwa02]).
![]() , we show the following strong (
, we show the following strong (![]() ) asymptotics of
the random vector
) asymptotics of
the random vector
![]() , where
, where
![]() denotes the number of nodes containing
denotes the number of nodes containing ![]() keys after
having introduced
keys after
having introduced ![]() keys in the tree: there exists deterministic
vectors
keys in the tree: there exists deterministic
vectors ![]() ,
, ![]() and
and ![]() and random variables
and random variables ![]() and
and ![]() such that
such that