DGGS - Geometry of Matrices

Differential Geometry and Geometric Structures

Main Page | Research Areas | Geometry of Matrices

	Geometry of Matrices The aim of the project is to study projective and affine matrix spaces and related questions in the research field of linear preserver problems.
	The Geometry of Matrices and Linear Preserver Problems
	Principal Investigator: Wen-ling Huang Austrian Science Fund (FWF) Lise Meitner fellowship M1023 Austrian Co-Applicant: Hans Havlicek
	Geometry of Matrices Related to his study of analytic functions of several complex variables, the Chinese mathematician L.K. Hua initiated the geometry of matrices in the middle forties of the last century. He studied four kind of matrix spaces: The space of m × n matrices of size over a division ring. The space of n × n Hermitian matrices over a division ring which is equipped with an an anti-automorphism whose square is the identity. The space of n × n symmetric matrices over a (commutative) field. The space of n × n alternate matrices over a (commutative) field. In all these spaces there is a binary adjacency relation. Various fundamental theorems describe all bijections between matrix spaces of the same kind which preserve adjacency in both directions. Projective matrix spaces Each of the above matrix spaces admits a projective closure. To mention just one example: The projective space of m × n matrices is the Grassmann space of m-dimensional subspaces of an (m + n)-dimensional vector space. Also here there is an adjacency relation and in most cases all adjacency preserving bijections are known.
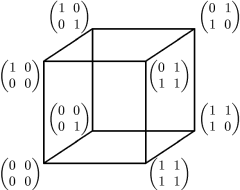
The space of symmetric 2 × 2 matrices over the Galois field with two elements.	Diameter preserving mappings Presently, we focus our attention on mappings on (projective) matrix spaces which preserve the diameter in both directions. However, our approach is more general, as we exhibit a class of (finite or infinite) graphs subject to certain restrictions and the diameter-preserving surjections between them. Then our graph-theoretical results are applied to various spaces of matrices. The image on the left hand side displays the graph on a matrix space, where a diameter preserving bijection need not preserve adjacency. Indeed, it suffices to exchange two points at distance 3, while all other points remain fixed. This peculiar property is due to the fact that alternate matrices over a field of characteristic 2 are symmetric.

Publications

H. Havlicek: On isomorphisms of Grassmann spaces, Mitt. Math. Ges. Hamburg 14 (1995), 117-120.
Preprint (PDF)
W.-l. Huang: Adjacency preserving transformations of Grassmann spaces. Abh. Math. Sem. Univ. Hamburg 68 (1998), 65-77.
W.-l. Huang: On the fundamental theorems of the geometries of symmetric matrices. Geom. Dedicata 78 (1999), 315-325.
W.-l. Huang: Adjacency preserving mappings of invariant subspaces of a null system. Proc. Am. Math. Soc. 08 (2000), 2451-2455.
W.-l. Huang: Characterization of the transformation group of the space of a null system. Res. Math. 40, 226-232 (2001).
W.-l. Huang and A. Schroth: Adjacency preserving mappings. Advances in Geometry 3 (2003), 53-59.
W.-l. Huang, Z.-X. Wan and R. Höfer: Adjacency preserving mappings of symmetric and Hermitian matrices. Aequationes Math. 67 (2004), 132-139.
W.-l. Huang and Z.-X. Wan: Adjacency preserving mappings of rectangular matrices. Beitr. Alg. Geom. 45 (2004), no. 2, 435-446.
A. Blunck and H. Havlicek: On bijections that preserve complementarity of subspaces, Discrete Math. 301 (2005), 46-56.
Preprint (PDF)
H. Havlicek and P. Šemrl: From geometry to invertibility preservers, Studia Math. 174 (2006), 99-109.
Preprint (PDF)
W.-l. Huang: Adjacency preserving mappings between point-line geometries. Innov. Incidence Geom. 3 (2006), 25-32.
W.-l. Huang and P. Šemrl: Adjacency preserving maps on Hermitian matrices. Canad. J. Math. 60 (2008), 1050-1066.
W.-l. Huang: Adjacency preserving mappings of 2 × 2 Hermitian matrices. Aequationes Math. 75 (2008), 51-64.
W.-l. Huang and H. Havlicek: Diameter preserving surjections in the geometry of matrices. Linear Algebra Appl. 429 (2008), 376-386.
Preprint (PDF)
A. Blunck and H. Havlicek: Projective lines over Jordan systems and geometry of Hermitian matrices, Linear Algebra Appl. 433 (2010), 672-680.
Preprint (PDF)