Differential Geometry and Geometric Structures

Main Page | Research Areas | Geometry and Quantum Theory

Geometry and Quantum Theory

Action Slovakia-Austria

Finite Geometries Behind Hilbert Spaces

Slovak head of project: Metod Saniga
Astronomický ústav
Slovenská akadémia vied
Tatranská Lomnica
Slovakia

Austrian head of project: Hans Havlicek

Supported by the Slovak and Austrian Governments
(Aktion Slowakei - Österreich), project number 58s2, 2007-2008.

Finite Projective Ring Geometries:

An Intriguing Emerging Link Between Quantum Information Theory, Black-Hole Physics, and Chemistry of Coupling

Cooperation group at the Centre for Interdisciplinary Research, University of Bielefeld (Germany)

August 1st to October 31st, 2009.

Principal Organiser: Hans Havlicek, Vienna University of Technology, Austria
Co-Organiser: Metod Saniga, Astronomical Institute of the Slovak Academy of Sciences, Tatranská Lomnica, Slovakia

Further Information

ZiF Cooperation Group 2009

Astronomical Institute

Astronomical Institute, Slovak Academy of Sciences

Finite Ring Geometries: Where Qudits meet Black Holes

Slovak head of project: Metod Saniga, Astronomický ústav, Slovenská akadémia vied, Tatranská Lomnica, Slovakia

Austrian participants: Hans Havlicek (head) and Boris Odehnal.

Supported under the Slovak-Austrian Science and Technology Cooperation Agreement under grants SK 07-2009 (Austrian side) and SK-AT-0001-08 (Slovak side), 2009-2010.

Finite-Geometrical Aspects of Quantum Theory

Principal Investigator: Metod Saniga (Lise Meitner research fellowship)

Co-applicant: Hans Havlicek

Supported by the Austrian Science Fund (FWF - Fonds zur Förderung der Wissenschaftlichen Forschung), project M-1564-N27, 2014-2015.

Workshop

Vienna University of Technology, February 23-27, 2015
Poster (PDF)

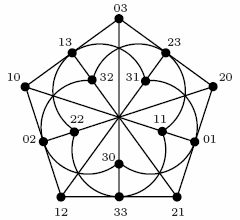
Doily

The smallest generalised quadrangle

Two-qubits and the smallest generalised quadrangle

M. Saniga and M. Planat discovered in 2006 that completely new vistas open up if, instead of dealing with a given Hilbert space itself, one considers the associated space of generalised Pauli operators/matrices. They demonstrated that the operators' space characterising the simplest non-trivial systems, so-called two-qubits, is isomorphic to the generalised quadrangle of order two.

The the generalised quadrangle of order two is a point-line geometry with 15 points and 15 lines. Each point is on 3 lines and, dually, also each line is incident with 3 points. Collinear points correspond to commuting operators.

Generalisations

Some steps to generalise the above Saniga-Planat Theorem have already been taken, thereby establishing a relationship to symplectic polar spaces (K. Thas).

We aim at further generalisations of this theorem to systems of N-qudits for arbitrary numbers N and d. Here the projective line over the ring of integers modulo d plays a prominent role.

Further Information

Visit the web site of Metod Saniga (external link).

Publications

H. Havlicek and K. Svozil: Density conditions for quantum propositions, J. Math. Phys. 37 (11) (1996), 5337-5341.
Preprint (PDF)
H. Havlicek, G. Krenn, J. Summhammer, and K. Svozil: Colouring the rational quantum sphere and the Kochen-Specker theorem, J. Phys. A 34 (2001), 3071-3077.
Preprint (PDF)
M. Saniga, M. Planat, P. Pracna, and H. Havlicek: The Veldkamp-space of two-qubits, SIGMA Symmetry Integrability Geom. Methods Appl. 3 (2007), paper 075, 7 pp. (electronic).
Preprint (PDF)
H. Havlicek and M. Saniga: Projective ring line of a specific qudit, J. Phys. A 40 (2007), F943-F952.
Preprint (PDF)
H. Havlicek and M. Saniga: Projective ring line of an arbitrary single qudit, J. Phys. A 41 (2008), Article ID 015302, 12 pp.
Preprint (PDF)
M. Saniga, H. Havlicek, M. Planat, and P. Pracna: "Twin Fano-Snowflakes" over the smallest ring of ternions, SIGMA Symmetry Integrability Geom. Methods Appl. 4 (2008), paper 050, 7 pp. (electronic).
Preprint (PDF)
H. Havlicek, B. Odehnal, and M. Saniga: Factor-group-generated polar spaces and (multi-)qudits, SIGMA Symmetry Integrability Geom. Methods Appl. 5 (2009), paper 096, 15 pp. (electronic).
Preprint (PDF) | Article (PDF, external link)
H. Havlicek, B. Odehnal, and M. Saniga: Möbius pairs of simplices and commuting Pauli operators, Math. Pannonica 21 (2010), 115-128.
Preprint (PDF)