|
Hans Havlicek: Advanced Descriptive Geometry
These lectures for students of Descriptive Geometry (teacher's programme) in their second year aim at giving an elementary, but rigourous, introduction to various concepts of Differential Geometry which are frequently used in Descriptive Geometry.
|
|
|
Contents
The subsequent list refers to my lectures in the years 1996-1997 according to the old curriculum.
|
|
1. Curves
Affine and cartesian coordinate systems, Curves in the Euclidean plane (parametrization, differentiability, regularity, tangents, arc-length, curvature, osculating circles, construction of Bereis), Curves in the Euclidean space (osculating plane, Frenet's basis, curvature, osculating circles), Implicitly defined curves in the plane. |
|
2. Surfaces
Surfaces in the Euclidean space (parametrisation, differentiability, regularity, tangent plane), Implicitly defined surfaces, The Theorem of Meusnier (Meusnier's sphere, asymptotic tangents), Dupin's indicatrix (normal curvature of tangents, classification of points on a surface), Surfaces contact along a common curve. |
|
3. Cones and Cylinders
Basic properties, Application: silhouette of surfaces, Development in the plane (isometric mappings, theorem of Catalan). |
|
4. Tangent Surfaces
Basic properties, development, indicatrices. |
|
|
5. Screw Motions
Orientation of the Euclidean space, Motions in space (rotations, screw motions, continuous motions), Screw curves, The 'Drehfluchtprinzip' of Th. Schmidt, Indicatrices of screw surfaces, Circular screw surfaces (screw pipe surfaces), Ruled screw surfaces (right helicoid). |
|
6. Ruled Surfaces
Torsal and non-torsal rulings, Conoidal surfaces, Torsal
surfaces, Isophotic curves on surfaces, Geometric lightning models. |
Frenet basis
|
Illustrations
The following material was prepared for these lectures with the computer algebra system 'Maple V'.
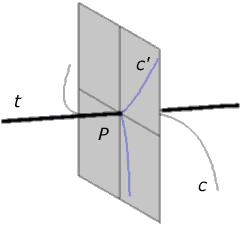
Orthogonal projection of a curve in the direction of a tangent. If we chose one point P on a given curve c then the orthogonal projection parallel to the tangent t at that point yields a curve c' (drawn in blue colour) in the plane through P which is perpendicular to the tangent t. The Taylor approximation of this planar curve (up to terms of fourth order) is Neil's parabola. This curve is also known under the name semicubic parabola.
The Frenet basis of the curve at the chosen point P is orthonormal and right handed. Its vectors span three mutually orthogonal lines through P viz. the tangent t and the two lines through P in the shaded plane. One of them is the tangent of the semicubic parabola c' at P; it lies in the osculating plane of c at the point P.
|
Right helicoid
|
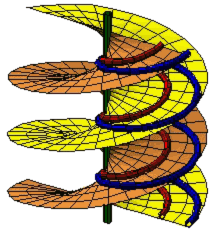
Screw curves on a right helicoid. A right helicoid is generated by a 'horizontal' line that meets the 'vertical' axis of a continuous screw motion. The various positions of the generating line yield the rulings of the helicoid.
Clearly, the path of each point is a screw curve, except for the points on the axis; their paths coincide with the axis. In particular, the points on the generating line yield a one-parameter family of screw curves on the right helicoid. These curves are the asymptotic curves of the surface other than its generators.
Somewhat surprisingly, there are also 'other' screw curves on the right helicoid!
Each of them arises as the intersection of the right helicoid with a cylinder of revolution containing the axis of the helicoid. The axis of such a cylinder can be chosen arbitrarily, whence there are infinitely many screw curves of this kind. The parameter of those 'other' screw curves is half of the parameter of the right helicoid. Two such curves (one in red and one in blue) are depicted in our illustration.
|
Circular screw surfaces
|
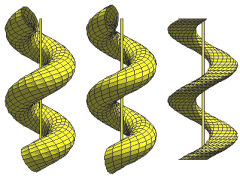
Three types of circular screw surfaces. Moving a circle under a continuous screw motion yields a circular screw surface. The shape of the surface depends on the position of the generating circle.
Our illustration shows three particular cases:
-
On the right hand side the plane of the circle is 'horizontal' (orthogonal to the 'vertical' axis of the screw motion).
-
In the middle the plane is 'vertical', i. e., it is parallel to the axis of the screw motion.
-
The surface on the left hand side is a screw pipe surface which is the envelope of a sphere subject to a continuous screw motion. In this case the generating circle is neither vertical nor horizontal.
Although, at a first glance, these three surfaces may look the same, their geometric properties are quite different.
|
Developable surface joining two circles
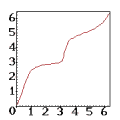
Velocity on the second circle
|
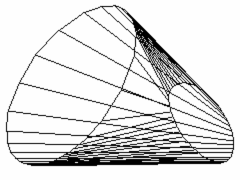
Joining two circles by a developable ruled surface. The problem is to find a developable ruled surface that connects two given circles lying in non-parallel planes.
In order to obtain the rulings of such a surface, one has to join points with coplanar tangents on the two circles. Two such tangents either have a point in common or they are parallel. The plane spanned by them is then a tangent plane of the linking ruled surface.
The first picture shows a wireframe model of one such surface. There is also another solution, however that surface has a self-intersection, whence it is of no use in applications.
If we think of a point moving on the circle on the right hand side with constant speed, then the corresponding point (on the left hand side) will not move with constant speed. The diagram below displays how the corresponding point moves when the first point goes once around its circle. The scaling is in terms of radians.
Instead of that complicated non-linear function one could also use the linear function y=x to define a one-one relation between the points of the given circles. However, by joining corresponding points one would get a non-developable surface which could not be made out of sheet-metal.
|

Isophotic patches
|
Isophotic patches on a surface of revolution. At each illuminated point, the shading of the surface is governed by the absolute value of the cosine of the angle formed by the line perpendicular to the surface and the light ray through this point.
-
absolute value of cosine = 1: full brightness
-
cosine = 0: no brightness, light rays are touching the surface.
In our illustration, showing a flower vase, we adopted a lightning model with a single light source at infinity. So all light rays are parallel to each other. Additionally, a very small amount of ambient (undirected) light is taken into account. Otherwise the non-illuminated points would appear in black colour.
|
|
Quick Links
H. Havlicek: Lineare Algebra für Technische Mathematik
(in German)
H. Havlicek: Multilinear Algebra
H. Havlicek: Evaluation of Teaching
Teaching
Sitemap
|

