DGGS - Hans Havlicek: Projective Geometry

Differential Geometry and Geometric Structures

Main Page | Staff | Hans Havlicek | Projective Geometry

	Hans Havlicek: Projective Geometry This series of lectures for students of Descriptive Geometry (teacher's programme) gives an introduction to projective, affine and Euclidean geometry.
	Contents The subsequent list refers to my lectures in the years 2001-2003 according to the old curriculum.
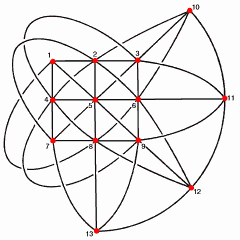
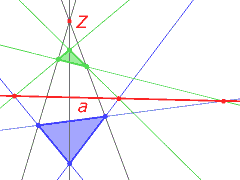
Projective plane with 13 points Axiom of Desargues	1. Affine and Projective Planes Axioms of affine and projective planes Connection between affine and projective planes Principle of duality 2. Projectivities and Collineations Perspectivities Projectivities Axioms of Desargues and Pappos Hessenberg's theorem Perspective and projective collineations Harmonic tetrads Fano's axiom 3. Affinities Perspectivities in affine planes Perspective and projective affinities 4. Conics Steiner's definition Pascal's theorem Projectivities on conics External and internal points Nuclei Polarity with respect to a conic Higher-order contact of conics Pencils of conics Conics in affine planes 5. Affine and Projective Spaces Axioms of affine and projective spaces Connection between affine and projective spaces 6. Properties of Projective Spaces Lattice of subspaces Dimension formula of Grassmann 7. Properties of Affine Spaces Parallel subspaces Hyperplane at infinity Affine geometry in projective terms 8. The Dual of a Projective Space Pencils of hyperplanes Dual space Principle of duality Bidual of a projective space 9. Projectivities and Collineations of Projective Spaces Projectivities Perspective and projective collineations Transitivity properties of the projective group
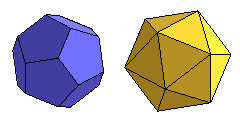
Dual polyhedra	10. Correlations Correlations Polarities Conjugate points Auto-polar simplices absolute points Types of polarities 11. Quadrics Quadratic sets Quadrics Polarity with respect to a quadric Common points of two conics Reguli Quadrics in affine spaces
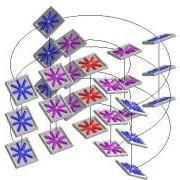
General linear complex of lines	12. Null Polarities and Line Geometry in 3-Spaces Null polarities in 3-spaces General and special linear complexes of lines Hyperbolic, parabolic, and elliptic congruences of lines 13. Twisted Cubics Seydewitz's definition Chords tangents and osculating planes Polarity with respect to a twisted cubic Cubic developables Axes
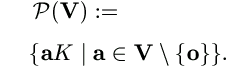
	14. Projective and Affine Spaces over Vector Spaces Projective spaces over vector spaces Fundamental theorem of projective geometry Affine spaces over vector spaces Fundamental theorem of affine geometry Representation of collineations and affinities in terms of semilinear mappings Projective and affine coordinates Cross ratios and affine ratios 15. Real and Complex Projective Spaces Separating quadruplets Complexification of real spaces Complex conjugate elements 16. Euclidean Spaces Orthogonality in terms of an absolute polarity Similarities Spheres Direct and opposite congruence transformations Euclidean spaces over vector spaces Angles and lengths Axes and umbilical points of quadrics Quadrics of revolution Foci of conics