|
Hans Havlicek: Geometric Laboratory
(Geometrisches Praktikum - Geometrie am PC)
|
|
|
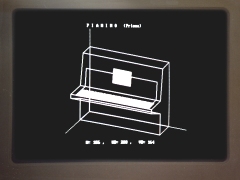
A photograph taken from the screen of the very first PC at the Institute of Geometry:
Resolution 640 x 400 pixels, black and white (Gunter Weiß, 1987)
|
Course
This computer based laboratory course for students of Descriptive Geometry (teacher's programme) was initiated by Professor Peter Paukowitsch and myself in the year 1987.
Later, there was a close co-operation with Gunter Weiß, who is now Professor of Geometry at the Dresden University of Technology. In particular, we developed a Turbo-Pascal unit ''GEO1.TPU'' allowing user-coordinates and an easy output on a plotter (using the language HPGL).
The plotters at that time were equipped with six or eight pens. It was always fascinating to watch them drawing, moving, and changing the pens. Needless to say, that we also had to develop our own handshaking protocol to avoid any overflow of the plotter's memory and a subsequent loss of data.
Lack of time made me finish my activities in the year 1990.
So this page is a nostalgic look back to the good old days when our personal computers had 640 kilobytes of memory, 10 megabyte hard disks (or two disk drives and no hard disk at all), and 8086 microprocessors with a CPU speed of 4.77 megahertz.
|


|
Some Pictures by my Students
The Turbo-Pascal programmes for creating the following pictures were written by my students Karin Baron, Claudia Grasser, Hannes Kuchler, Claudia Langmüller, Barbara Moser, Marianne Sames, Martin Walter, and Reinhard Wolfmayr.
Some of their original pictures have been slightly modified for this presentation.
Peano curves.
Peano curves are continuous curves that fill a region of the plane. They are named after the Italian mathematician Giuseppe Peano (1858-1932).
The first picture shows a meander-like polygon which is in some sense close to a Peano curve filling a square. By an iterative process, a Peano curve may be obtained from this polygon.
Secondly, a polygon is displayed which approximates a Peano curve filling an isosceles triangle. The segments of this polygon are actually very short, whence the polygon looks rather like a union of circular arcs, but this is not the case.
This Peano curve is attributed to the German mathematician Konrad Knopp (1882-1957).
|
|

|
Snowflakes. Another example of a pathological curve in the plane is Koch's snowflake curve, carring the name of Helge von Koch (1870-1924), a mathematician from Sweden.
As before, the picture gives just a rough approximation. The next step towards the real snowflake curve would be to subdivide each segment of the boundary into three congruent segments, and to replace each middle segment with two sides of an equilateral triangle pointing outside.
The snowflake curve has a very strange property: It has infinite length, although it is the boundary of a domain with finite area!
|
|

|
Mathematical trees.
This is a very simple mathematical model of a tree in two dimensions.
Each branch bifurcates in two smaller branches. All Y-shaped sub-figures are similar to each other.
The student, who made this image, was strongly reminded of broccoli (brassica oleracea). This could explain, why she decided to choose a green colour.
|
|
|
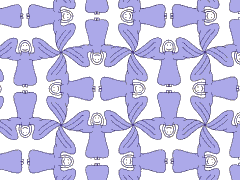
Wallpaper groups. A discrete group of isometries of the Euclidean plane which stabilises neither a point nor a line is called a wallpaper group.
There are seventeen wallpaper groups for the plane, one of them was used to create this Christmas card.
The action of the wallpaper group on one half of an angel yields infinitely many angles. This group contains, among other transformations, line reflections and rotations of 90 degrees.
|

|
Lissajous curves.
The first picture shows a curve of Lissajous type with parametric representation
x = sin at, y = cos bt,
where a = 3, b = 7, and t ranges in the real numbers.
As the sine and and cosine function are periodic, and since 3 : 7 is a rational ratio, the curve is closed.
An irrational ratio a : b would lead to a Lissajous curve filling a square.
The curves of this kind are named after the French physicist Jules Antoine Lissajous, who lived from 1822 to 1880.
|
|
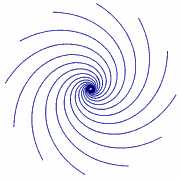
Logarithmic spirals. Next, you can see a family of logarithmic spirals which are winding around a common asymptotic point A. They will never reach this point. These logarithmic spirals are orbits of a one-parameter group of Euclidean similarities fixing the point A.
Every line through the asymptotic point A is an isogonal trajectory of this family of spirals, i. e., the line meets each of the spirals under a constant angle. It suffices to show this property for one line through the asymptotic point A. Due to the fact that the one-parameter group mentioned above acts transitively on the set of lines through the asymptotic point, every other line through A has also to be an isogonal trajectory.
|
|
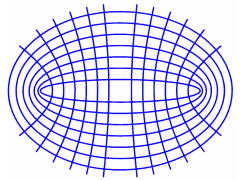
Orthogonal trajectories - confocal conics. Finally, two families of conics are displayed. All conics share two common foci. One family is formed by ellipses and the other by hyperbolas.
Observe that the ellipses are orthogonal trajectories of the hyperbolas, and vice versa. This means that every ellipse and every hyperbola meet orthogonally at each point of intersection.
Similarly, all parabolas with a common focus and a common axis fall into two families, each of which consists of orthogonal trajectories of the other family.
|
|
Quick Links
H. Havlicek: Lineare Algebra für Technische Mathematik
(in German)
H. Havlicek: Evaluation of Teaching
Teaching
Sitemap
|

