|
Affine Differential Geometry
In affine differential geometry a main point of research is the investigation of special models of surfaces in three dimensional affine space.
|
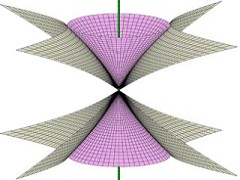
Algebraic affine surface of revolution with vanishing affine Gauss-Kronecker curvature.
|
Affine surfaces or revolution are characterised by affine surface normals intersecting a straight line.
Within this class of surfaces one can figure out those having additional properties, as e. g. flat affine metric, or vanishing (constant) affine mean curvature or affine Gauss curvature.
|
|
|
Publications
- F. Manhart.
Bonnet-Thomsen surfaces in Minkowski geometry. J. Geom. 106 (2015), 47-61.
- F. Manhart.
Affine Geometry of Minkowski Minimal Surfaces in ℝ13.
KOG 11 (2007), 15-23.
-
F. Manhart.
Affine surfaces with planar affine normals in 3-dimensional Minkowski space ℝ13.
Math. Pannon. 17/1 (2006), 69-82.
-
M. Peternell and F. Manhart.
The convolution of a paraboloid and a
parametrized surface.
J. Geom. Graphics 7 (2003), 157-171.
-
F. Manhart.
Affine rotational surfaces with vanishing affine curvature.
J. Geom. 80 (2004), 166-178.
-
F. Manhart.
Surfaces with affine rotational symmetry and flat affine metric in ℝ3.
Studia Sci. Math Hungarica 40 (2003), 1-10.
-
F. Manhart.
Die Flächen mit geraden Linien als affinen Zentraflächen.
J. Geom. 69 (2000), 166-171.
[MR].
-
F. Manhart.
Zur affinen Krümmungstheorie euklidischer Minimalflächen.
In 107 Jahre Drehfluchtprinzip (Vorau, 1997), pages 121-130. Tech.
Univ. Graz, Graz, 1999.
[MR].
-
F. Manhart.
Zur affinen Krümmungstheorie der Minimalflächen von G. Thomsen.
In Proceedings of the 4th International Congress of Geometry (Thessaloniki,
1996), pages 271-280. Giachoudis-Giapoulis, Thessaloniki, 1997.
[MR].
-
F. Manhart.
Die Affinminimalrückungsflächen.
Arch. Math. (Basel) 44 (1985), 547-556.
[MR].
|
|
Quick Links
Friedrich Manhart
Discrete Differential Geometry
Sitemap
|

 Technische Universität Wien
Technische Universität Wien
