|
Veronese Varieties
The aim of this project is to discuss Veronese varieties over a commutative ground field with non zero characteristic.
|
|
Veronese Varieties over Fields with non zero Characteristic
|
|
|
Principal Investigator: Hans Havlicek
Austrian Science Fund (FWF) project P12353-MAT
|
|
City of Vienna
|
Supported by the City of Vienna (Hochschuljubiläumsstiftung der Stadt Wien), project H-39/98.
|
Roman surface
|
The Roman Surface of J. Steiner
The Veronese surface in PG(5,ℝ) (the 5-dimensional projective space over the field ℝ of real numbers) is the image of a real projective plane PG(2,ℝ) under the quadratic Veronese mapping. On the left hand side you can see a picture of that Veronese surface which is obtained by a projection from 5-space onto a plane. Also, you can see the Veronese image of a line of PG(2,ℝ). All lines of PG(2,ℝ) go over to conics on the Veronese surface; the planar picture of those conics are ellipses and (at certain exceptional positions) line segments.
However our picture allows also another interpretation: First the Veronese surface is mapped under a suitable projection onto a surface of PG(3,ℝ) which was found (long before the Veronese surface) by Jacob Steiner while staying in Rome in the year 1844. Then this Steiner surface in 3-space is projected onto a plane. Observe that Steiner's surface has self intersections.
|
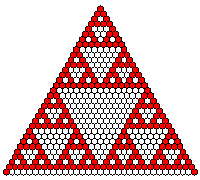
Pascal's triangle modulo 2
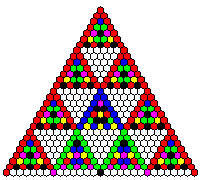
Pascal's triangle modulo 7
|
Nuclei of Normal Rational Curves
It is well known that all tangents of a conic are concurrent if, and only if, the characteristic of the ground field F equals two. This has lead to the concept of a nucleus. Furthermore, if the ground field F is finite and "small" (with respect to the dimension of the space), then additional properties of Veronese varieties arise.
A k-nucleus of a normal rational curve in an n-dimensional projective space over a commutative field F is the intersection over all k-dimensional osculating subspaces of the curve, where k = -1, 0, ..., n-1. It is well known that for characteristic zero all nuclei are empty.
In case of characteristic p > 0 and #F > n-1 the number of non zero digits in the representation of n+1 in base p equals the number of distinct nuclei. We have found a rather involved explicit formula expressing the dimensions of k-nuclei. It depends on the zero entries in Pascal's triangle modulo p.
The pictures on the left hand side show:
-
Lines 0, 1, ..., 32 of Pascal's triangle modulo 2.
-
Lines 0, 1, ..., 28 of Pascal's triangle modulo 7.
Residue classes are encoded by colours: 0 = white, 1 = red etc.
|
|
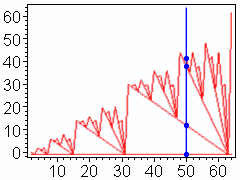
An Example
The diagram shows the dimensions of nuclei of a normal rational curve for characteristic p = 2. Horizontally, you can read off the (projective) dimension n = 2, 3, ..., 64 of the space, vertically you can see the dimensions of distinct nuclei of a normal rational curve.
For example, let p = 2 and n = 50:
The representation of 50+1 in base 2 is (110011); there are four non zero digits. So there are four distinct nuclei, including one empty nucleus. The following table gives exact values:
| k |
Dimension of k-nucleus |
| -1, 0, ..., 30 |
-1 |
| 31, 32, ..., 46 |
12 |
| 47, 48 |
38 |
| 49 |
42 |
|
Giuseppe Veronese
|
The Nucleus of a Veronese Variety
The ambient space of a Veronese variety Vmt has (projective) dimension
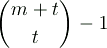
The nucleus of a Veronese variety Vmt is the intersection over all its osculating hyperplanes. For normal rational curves (m = 1, t = n) this nucleus is the (n - 1)-nucleus from above.
If the ground field F has characteristic p> 0 and sufficiently many elements, then the dimension of the nucleus of a Veronese variety Vmt is given by
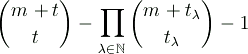
where
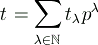
is the expansion of t in base p.
|
Graph of the function f
|
Multinomial Coefficients
For a fixed prime p, the codimension of the nucleus of a Veronese variety Vmt depends only on the function f that maps (m,t) to
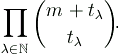
This product is just the number of multinomial coefficients
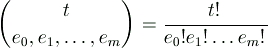
that do not vanish modulo p (F.T. Howard, 1974).
The picture on the left hand side shows the graph of this function for p = 3 and m, t = 1,2,...,25 with a logarithmic scaling along the vertical axis. If t is constant and m varies, then one moves along one of the valleys or mountain-ridges, otherwise (m constant and t variable) there are many ups and downs.
|
Pascal's pyramid modulo 2
|
Pascal's Pyramid
The array of 3-multinomial (trinomial) coefficients is Pascal's pyramid.
In our picture we use rhombic dodecahedra to illustrate the non zero entries in Pascal's pyramid modulo 2, whereas the positions of zero entries are left free.
Observe that here different colours have been chosen just for the sake of visualisation. All non zero entries at the same horizontal level (t = 0,1,...,16) share a common colour.
Each of the three faces equals Pascal's triangle modulo 2 which is illustrated above using a different colouring scheme.
We learned about this beautiful geometric representation of trinomial coefficients from Hans Walser (Switzerland).
|
|
|
Publications
-
H. Havlicek: Hyperoskulierende Kegelschnitte in Pappos-Ebenen der Charakteristik zwei, Sb. Österr. Akad. Wissensch., math.-naturw. Kl., Abt.II. 198 (1989), 141-146.
Preprint (PDF)
-
H. Havlicek: The Veronese surface in PG(5,3) and Witt's 5-(12,6,1) design, J. Comb. Theor. Ser. A. 84 (1998), 87-94.
Preprint (PDF)
-
H. Havlicek: Giuseppe Veronese and Ernst Witt - neighbours in PG(5,3), Aequat. Math. 58 (1999), 85-92.
Preprint (PDF)
-
J. Gmainer: Rationale Normkurven in Räumen positiver Charakteristik, Doctoral thesis, Vienna University of Technology, 1999.
-
J. Gmainer and H. Havlicek: Nuclei of normal rational curves, J. Geometry 69 (2000), 117 - 130.
Preprint (PDF)
-
J. Gmainer and H. Havlicek: A dimension formula for the nucleus of a Veronese variety, Linear Algebra Appl. 305 (2000), 191-201.
Preprint (PDF)
-
J. Gmainer: Pascal's triangle, normal rational curves, and their invariant subspaces, Eur. J. Comb. 22 (2001), 37-49.
Preprint (PDF)
-
H. Havlicek: Veronese varieties over fields with non-zero characteristic - a survey, Discrete Math. 267 (2003), 159-173.
Preprint (PDF)
|
|
Quick Links
Johannes Gmainer
Hans Havlicek
Design Theory
Geometry over Skew Fields
Sitemap
External Links

Austrian Science Fund (FWF)
|


