|
Welcome to the research group
Differential Geometry and Geometric Structures
|
|

Members & friends of the group in Jul 2021
photograph © by Narges Lali
|
Differential geometry has been a thriving area of research
for more than 200 years, employing methods from analysis
to investigate geometric problems. Typical questions
involve the shape of smooth curves and surfaces and the
geometry of manifolds and Lie groups. The field is at
the core of theoretical physics and plays an important
role in applications to engineering and design.
Finite and infinite geometric structures are ubiquitous
in mathematics. Their investigation is often intimately
related to other areas, such as algebra, combinatorics or
computer science.
These two aspects of geometric research stimulate and
inform each other, for example, in the area of "discrete
differential geometry", which is particularly well suited
for computer aided shape design.
|
|
Gallery of some research interests and projects

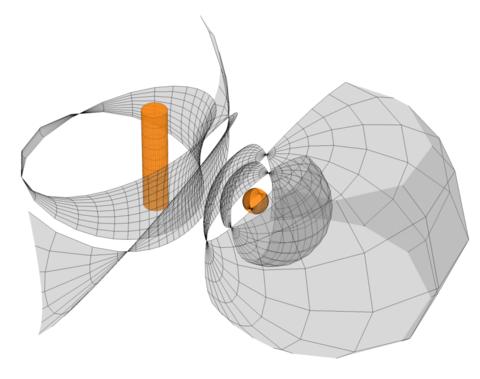
Symmetry breaking in geometry:
We discuss a geometric mechanism that may,
in analogy to similar notions in physics,
be considered as "symmetry breaking" in geometry.
(Fuchs, Hertrich-Jeromin, Pember;
Fig ©Nimmervoll)
Cyclic coordinate systems:
an integrable discretization in terms of a discrete flat
connection is discussed.
Examples include systems with discrete flat fronts or
with Dupin cyclides as coordinate surfaces
(Hertrich-Jeromin, Szewieczek)

We study surfaces with a family of
spherical curvature lines
by evolving an initial spherical curve through
Lie sphere transformations,
e.g., the Wente torus
(Cho, Pember, Szewieczek)
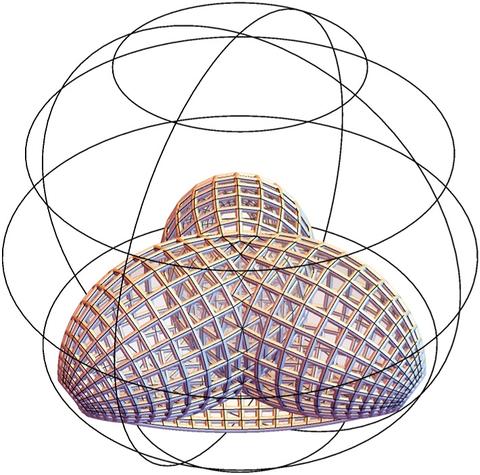
Discrete Weierstrass-type representations
are known for a wide variety of discrete surfaces classes.
In this project, we describe them in a unified manner,
in terms of the Omega-dual transformation applied to
to a prescribed Gauss map.
(Pember, Polly, Yasumoto)
Billiards:
The research addresses invariants of trajectories of a
mass point in an ellipse with ideal physical reflections
in the boundary. Henrici's flexible hyperboloid paves the
way to transitions between isometric billiards in ellipses
and ellipsoids (Stachel).

Spreads and Parallelisms:
The topic of our research are connections among spreads
and parallelisms of projective spaces with areas like
the geometry of field extensions, topological geometry,
kinematic spaces, translation planes or flocks of quadrics.
(Havlicek)

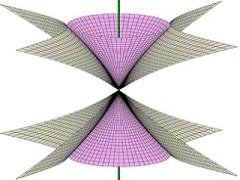
This is a surface of (hyperbolic) rotation in hyperbolic
space that has constant Gauss curvature,
a
recent classification project.
(Hertrich-Jeromin, Pember, Polly)

Geometric shape generation:
We aim to understand geometric methods to generate
and design (geometric) shapes,
e.g., shape generation by means of representation formulae,
by transformations, kinematic generation methods, etc.
(Hertrich-Jeromin, Fig Lara Miro)
Affine Differential Geometry:
In affine differential geometry a main point of research is
the investigation of special surfaces in three dimensional
affine space.
(Manhart)
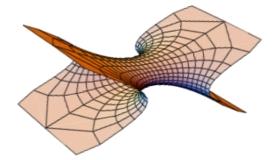
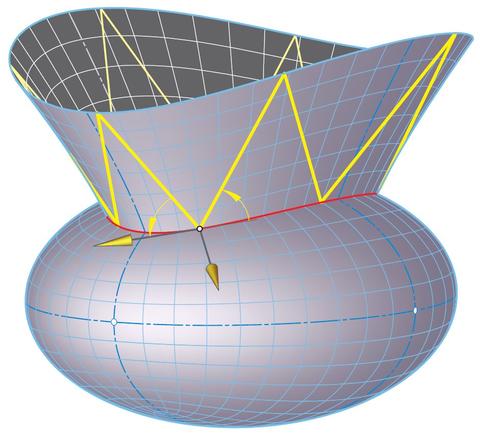
Transformations & Singularities:
We aim to understand how transformations of particular
surfaces behave (or fail to behave) at singularities, and
to study how those transformations create (or annihilate)
singularities.
The figure shows the isothermic dual of an ellipsoid,
which is an affine image of a minimal
Scherk tower.
(Hertrich-Jeromin)
|
|
News
- 27 Jun 2024: Geometry seminar
- Ilya Kossovskiy (Masaryk University in Brno and TU Wien):
Sphericity and analyticity of a strictly pseudo-convex hypersurface in
low regularity
Abstract
It is well known that the sphericity of a strictly pseudoconvex
CR-hypersurface amounts to the vanishing of its Chern-Moser
tensor. The latter is computed pointwise in terms of the 6-jet
of the hypersurface at a point, and thus requires regularity of
the hypersurface of class at least C^6.
In our joint work with Zaitsev, we apply our recent theorem on
the analytic regularizability of a strictly pseudoconvex
hypersurface to find a necessary and sufficient condition for
the sphericity of a strictly pseudoconvex hypersurfaces of
arbitrary regularity starting with C^2. Further, we obtain a
simple condition for the analytic regularizability of
hypersurfaces of the respective classes. Surprisingly, despite
of the seemingly analytic nature of the problem, our technique
is geometric and is based on the Reflection Principle in SCV.
- 20 Jun 2024: Geometry seminar
- Denis Polly (TU Wien):
Linear Weingarten surfaces in isotropic spaces
Abstract
According to a result by Burstall, Hertrich-Jeromin and Rossman,
linear Weingarten surfaces in Riemannian and Lorentian space
forms are the envelopes of isothermic sphere congruences with
constant curvature. This description is derived via the use of
Lie sphere geometry (LSG) and symmetry breaking to obtain
results about metric subgeometries of LSG. While this method
recovers all linear Weingarten surfaces in Riemannian and
Lorentzian space forms, surfaces in isotropic space, as
described by Strubecker, do not appear. Our goal is to close
this gap.
To this end, we introduce a way of breaking symmetry that has
not recieved much attention. This leads us to the study of
isotropic space forms and the linear Weingarten surfaces
therein. As an application we describe Weierstrass-type
representations for certain linear Weingarten surfaces in these
space forms.
- 13 Jun 2024: Geometry seminar
- Fabian Achammer (TU Wien):
Formula equations and the affine solution problem
Abstract
Formula equations are certain kinds of equations whose solutions
are logical formulas.
They serve as a common framework for many different problems in
computational logic, ranging from software verification to
inductive theorem proving.
We start with a short introduction to mathematical logic and
computational problems, then introduce formula equations and
give a glimpse of their wide applicability.
In the main part of the talk we explore the solution of a
particular problem in the area of formula equations - the affine
solution problem - which translates into a problem about affine
spaces.
Finally, we discuss some results surrounding a generalization of
the affine solution problem, which is still open, namely the
convex solution problem which is a computational problem about
convex polytopes.
- 06 Jun 2024: Geometry seminar
- Kiumars Sharifmoghaddam (TU Wien):
Rigid-foldable Quad Meshes with Control Polylines: Interactive Design and Motion Simulation
Abstract
Generic discrete surfaces composed of quadrilateral plates connected by
rotational joints in the combinatorics of a square grid are rigid, but
there also exist special ones with 1-parametric flexibility. This
dissertation focuses on two particular classes of so-called T-hedra
(trapezoidal quad surfaces) and V-hedra (discrete Voss surfaces).
T-hedra can be thought of as a generalization of discrete surfaces of
revolution in such a way that the axis of rotation is not fixed at one
point but rather sweeping a polyline path on the base plane. Moreover,
the action does not need to be a pure rotation but can be combined with
an axial dilatation. After applying these transformations to the
breakpoints of a certain discrete profile curve, a flexible quad-surface
with planar trapezoidal faces is obtained. Therefore, the design space
of T-hedra also includes as subclasses discretized translational
surfaces and moulding surfaces beside the already mentioned rotation
surfaces. V-hedra are the discrete counterpart of Voss surfaces which
carry conjugate nets of geodesics. In discrete case the opposite
interior angles of a vertex star are equal. From a V-hedral vertex one
can always generate an anti-V-hedral vertex with the same kinematics, in
which the sum of corresponding opposite angles equal to pi and therefore
is a known case of valence four flat-foldable and developable origami
vertex. The author developed Rhino/Grasshopper plugins, implemented with
C-sharp, which make the design space of T-hedra, V-hedra and
anti-V-hedra accessible for designers and engineers. The main components
enable the user to design these quad surfaces interactively and
visualize their deformation in real time based on a recursive
parametrization of the quad-mesh vertices under the associated isometric
deformation. Furthermore, this research investigates semi-discrete
T-hedral surfaces and other topologies, such as tubular structures
composed of T-hedra.
- 23 May 2024: Geometry seminar (14:30 Dekanatsraum 9th floor)
- Georg Nawratil (TU Wien):
A global approach for the redefinition of higher-order flexibility and rigidity
Abstract
The famous example of the double-Watt mechanism given by Connelly and Servatius [Higher-order rigidity - What is the proper definition? Discrete & Computational Geometry 11:193-200, 1994] raises some problems concerning the classical definitions of higher-order flexibility and rigidity, as they attest the cusp configuration of the mechanism a third-order rigidity, which conflicts with its continuous flexion. Some attempts were done to resolve the dilemma but they could not settle the problem. According to Müller [Higher-order analysis of kinematic singularities of lower pair linkages and serial manipulators. Journal of Mechanisms and Robotics 10:011008, 2018] cusp mechanisms demonstrate the basic shortcoming of any local mobility analysis using higher-order constraints. Therefore we present a global approach inspired by Sabitov's finite algorithm for testing the bendability of a polyhedron given in [Local Theory of Bendings of Surfaces. Geometry III, pp. 179-250, Springer, 1992], which allows us (a) to compute iteratively configurations with a higher-order flexion (e.g. all configurations of a given 3-RPR manipulator with 3rd-order flexion) and (b) to come up with a proper redefinition of higher-order flexibility and rigidity.
- 16 May 2024: Geometry seminar
- Martina Iannella (TU Wien):
Classification of non-compact $3$-manifolds
Abstract
A classification problem consists of an equivalence relation on
some set of mathematical objects; a solution to such a problem
is an assignment of complete invariants. In this talk we
consider the problem of classifying non-compact 3-manifolds up
to homeomorphism from the perspective of descriptive set theory.
We first look at the parametrization of 3-manifolds as objects
of a Borel subset of a Polish space. We then discuss the
framework of Borel reducibility, a standard tool for comparing
the complexity of different classification problems, and present
our recent result which determines the exact complexity of the
classification of non-compact 3-manifolds up to homeomorphism.
This is joint work with Vadim Weinstein.
- 02 May 2024: Geometry seminar
- Niklas Affolter (TU Wien):
Discrete maximal Lorentz surfaces and incircular nets
Abstract
Incircular nets (s-embeddings) were introduced by Chelkak as a
generalization of Smirnov's approach to study the conformal
invariance of the Ising model in the continuous limit. We build
upon the work of Chelkak, Laslier and Russkikh to present a
class of incircular nets that corresponds to discrete isothermic
surfaces in Lorentz space. As a special case, we identify
discrete maximal surfaces, which are discrete surfaces with
vanishing discrete mean curvature. In this way, we introduce a
result on the discrete level that was obtained by CLR in the
limit. We also introduce an associated family of discrete
maximal surfaces and the corresponding family of incircular
nets. Joint work with Dellinger, Müller, Polly, Smeenk and
Techter.
- 25 Apr 2024: Geometry seminar
- Alessandro Andretta (University of Turin):
The Banach-Tarski paradox
Abstract
One of the most surprising results of modern mathematics is the
following result proved by Hausdorff, Banach and Tarski:
the unit ball of the euclidean space can be partitioned in a
finite number of pieces so that these can be rearranged, using
rigid motions so to form two balls identical to the original.
The proof is non-constructive, relying on the Axiom of Choice,
and the pieces of the decomposition are inconceivably sharp and
edgy!
Geometry plays a substantial role, as the core of the proof is
based on the existence of a free subgroup of the group of
rotations.
(A similar result cannot be proved for the plane, i.e. it is not
possible to duplicate a disk.)
In this talk I will sketch the proof of the Banach-Tarski
paradox, and survey many related results that have been proved
in the following years.
18 Apr 2024: Geometry seminar - Ivan Izmestiev (TU Wien): Cayley-Bacharach theorem and sums of squares
Abstract
The Cayley-Bacharach theorem (first proved by Chasles) says that
if two cubics meet at nine points, then any other cubic passing
through eight of these nine points also passes through the
ninth. This theorem includes as special cases the Pappus and the
Pascal theorems.
The sums of squares problem was posed by Hilbert: can every
positive definite homogeneous polynomial of degree $2d$ in n
variables be represented as a sum of squares of polynomials of
degree $d$? While the answer is positive for $d=1$ and n arbitrary
as well as for d arbitrary and $n=2$, Hilbert has proved the
negative for $d=3$ and $n=3$. And a crucial point in his proof was
the Cayley-Bacharach theorem.
This talks is based on the articles by Eisenbud-Green-Harris and
Blekherman.
- 21 Mar 2024: Geometry seminar
- Gudrun Szewieczek (TU Munich):
Discrete isothermic nets with a family of spherical parameter lines from holomorphic maps
Abstract
Smooth surfaces with a family of planar or spherical curvature
lines are an active area of research, driven by both purely
differential geometric aspects and practical applications such
as architectural design. In integrable geometry it is a natural
question to ask which of these surfaces admit a conformal
curvature line parametrization and are therefore isothermic
surfaces.
It is an open problem to explicitly describe all those smooth
isothermic surfaces. However, over time, prominent examples were
found in this rich integrable surface class: above all Wente's
torus. More recently, further specific examples have led to the
discovery of compact Bonnet pairs and to free boundary solutions
for minimal and CMC-surfaces.
This talk covers a discrete version of the problem: we shall
generate all discrete isothermic nets with a family of spherical
curvature lines from special discrete holomorphic maps via the
concept of "lifted-folding".
In particular, we point out how this novel approach leads to
quasi-periodic solutions and to topological tori with
symmetries.
This is joint work with Tim Hoffmann.
- 14 Mar 2024: Geometry seminar (Sem.R. DB gelb 03)
- David Sykes (TU Wien):
CR Hypersurface Geometry, an Introduction
Abstract
CR geometry concerns structures on real submanifolds in complex
spaces that are preserved under biholomorphisms. This talk will
present a light introduction to CR geometry of real
hypersurfaces. We will survey some of the area's major
classical results, namely solutions to local equivalence
problems of E Cartan, Tanaka, and Chern-Moser and their
applications. And we will preview some of the area's current-day
research trends related to Levi degenerate structures.
|

 Technische Universität Wien
Technische Universität Wien