|
Elementary Geometry
For any researcher with a love of geometry, enticing problems remain.
|
|
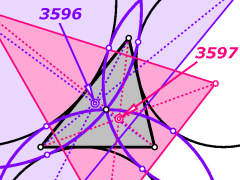
The Odehnal points
B. Odehnal. Some triangle centers associated with the circles tangent to the excircles. Forum Geometricorum 10 (2010), 35-40.
Among the eight circles touching all three excircles of a triangle we find the three side lines, the Feuerbach circle, and its inverse with respect to the radical circle of the excircles.
The remaining three tritangent circles have a common point, i.e., the Spieker centre. Their contact points with those excircles which are enclosed by them form a triangle which is in perspective with the base triangle. The centre of perspectivity is the first Odehnal point X3596. The centres of these three tritangent circles form a triangle which is also in perspective with the base triangle. The centre of perspectivity is the second Odehnal point X3597.
|
|
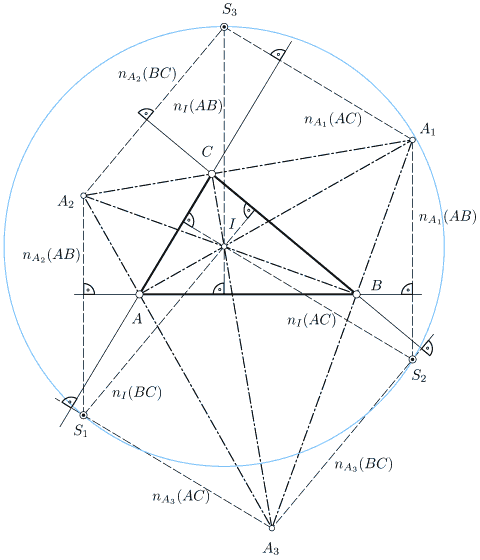
B. Odehnal. Three points related to the incenter and excenters of a triangle. Elem. Math. 61/2 (2006), 74-80.
In the present paper it is shown that certain normals to the sides of a triangle A,B,C passing through the excentres A1, A2, A3, and the incentre I are concurrent. The triangle built by these three points (S1,S2,S3) has the incenter of A,B,C for its circumcentre. The radius of the circumcircle is twice the radius of the circumcircle of A,B,C. Some other results concerning the triangle S1, S2, S3 are stated and proved.
|
|
|
Publications
-
H. Stachel. Zu K. Schüttes Verallgemeinerung des Satzes von Napoleon. Elem. Math. 46 (1991), 25-27.
-
H. Stachel. The HEUREKA-polyhedron. In K. Böröcky and G. Fejes Tóth, editors, Intuitive geometry (Szeged, 1991), volume 63 of Colloq. Math. Soc. János Bolyai,
pages 447-459. North-Holland, Amsterdam, 1994, ISBN 0-444-81906-1.
Proceedings of the 3rd international conference held in Szeged, Hungary, Sept. 2-7 1991.
-
H. Stachel.
Napoleon's theorem and generalizations through linear maps.
Beitr. Algebra Geom. 43 (2002), 433-444.
-
H. Havlicek and G. Weiß: Ecken- und Kantenhöhen im Tetraeder, KoG 6 (2002), 71-80.
Preprint (PDF)
-
H. Havlicek and G. Weiß: Altitudes of a tetrahedron and traceless quadratic forms, Amer. Math. Monthly 110 (2003), 679-693.
Preprint (PDF)
-
R. Riesinger: On Wallace loci from the projective point of view, J. Geom. Graphics 8 (2004), 201-213.
-
B. Odehnal. Three points related to the incenter and excenters of a triangle. Elem. Math. 61/2 (2006), 74-80.
-
S. Abu-Saymeh, M. Hajja, H. Stachel.
Another cubic associated with the triangle. J. Geom. Graphics 11, 15-26 (2007).
-
B. Odehnal. Some triangle centers associated with the circles tangent to the excircles. Forum Geometricorum 10 (2010), 35-40.
-
B. Odehnal. Generalized Gergonne and Nagel Points. Beitr. Algebra Geom. 51/2 (2010), 477-491.
-
B. Odehnal. Equioptic points of a triangle. Proc. 14th Internat. Conf. Geometry Graphics, Aug. 4-8, 2010, Kyoto/Japan, article No. 197, ISBN 978-4-9900967-1-7.
-
B. Odehnal. Equioptic curves of conic sections. J. Geom. Graphics 14/1 (2010), 29-43.
-
B. Odehnal. Poristic Loci of Triangle Centers. J. Geom. Graphics 15/1 (2011), 45-67.
|
|
|
Quick Links
Hans Havlicek
Boris Odehnal
A Tribute to Rolf Riesinger (1945-2018)
Hellmuth Stachel
Sitemap
External Links
Gunter Weiß, Dresden University of Technology
Poster
Elementargeometrie
(PDF - in German/English)
|
