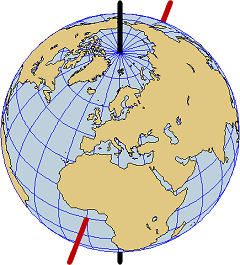
The axis of the earth (black) and the axis of a projection with transverse aspect (red)
|
Axis of a Projection
The axis of the earth joins the north pole with the south pole. With any map projection one can associate an axis which joins a distinguished point of the globe with its antipodal point.
Normal Aspect
Normal aspect means that the two axes coincide.
For example, under conical and azimuthal projections the north pole will always be displayed in the centre of the map. On the other hand, cylindrical and pseudo-cylindrical projections display another point in the centre of the map, namely the point (0° E, 0° N), i. e., the point where the meridian of Greenwich meets the equator.
Transverse Aspect
Here the axis of the projection belongs to the plane of the equator.
In all our maps the point off the African coast with geographical coordinates (0° E, 0° N) takes over the role of the north pole.
|
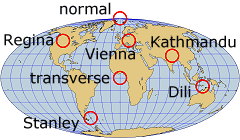
Aspects of our map projections
|
Oblique Aspect
If the axis of the projection is neither normal nor transverse then one speaks of an oblique aspect.
Our series of pictures are based on axes through one of the following cities:
-
Vienna (16°E, 48°N), Austria
-
Kathmandu (85°E, 28°N), Nepal
-
Dili (126°E, 9°S), Timor-Leste
-
Regina (105°W, 50°N), Saskatchewan, Canada
-
Stanley (60°W, 52°S), Falkland Islands
Other Settings
Rotation
This will rotate the globe about the axis of projection by 0°, 90°, 180° or 270° before it is displayed. The effect is a change of the image, which depends on the chosen projection.
Display
-
Standard: A part of the globe (e. g. a hemisphere) is displayed.
-
Wide: The entire globe is displayed or, if this is impossible, at least a wide part thereof.
For some projections there will be no difference between the two pictures, because both of them display the entire earth.
|

 Technische Universität Wien
Technische Universität Wien
