|
|
Die Sammlung mathematischer Modelle
am Institut für Diskrete Mathematik und Geometrie
|
|
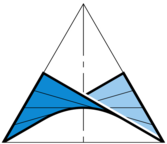
Raumkurve 4.Ordnung (mit abwickelbarer Fläche) (#111) |
|
Beschreibung:
|
| Das Fadenmodell der Raumkurve vierter Ordnung erster Art und ihrer abwickelbaren Fläche soll die Haupteigenschaften derjenigen Raumkurven vierter Ordnung, die der Schnitt der Flächen zweiter Ordnung eines Büschels sind, sowie der abwickelbaren Fläche ihrer Tangenten und der Doppelkurve dieser Flächen, zur Anschauung
bringen. Die Kurve liegt auf zwei reellen und zwei imaginären Kegeln. Die Darstellung erfolgt als Schnitt jener beiden. Das Modell zeigt zugleich die abwickelbare Fläche ihrer Tangenten. |
| Fachgebiete: |
| Raumkurven |
| Kataloge: |
Martin Schilling, Catalog mathematischer Modelle, 7. Auflage, Leipzig 1911, S.24 und S.134
Katalognummer: 201 |
| Vertrieb und Hersteller: |
Verlagshandlung Martin Schilling Leipzig;
H. Wiener
Veröffentlichungsdatum: Veröffentlicht 1884 |
|
| Material und Maße: (h x b x t) |
|
Metall, Fäden
x x cm, Gramm |
|
|
Navigation
Die Modelle
Die Geschichte der Sammlung
Literatur
Kontakt
Links
Quick Links
Sitemap
|
Technische Universität Wien
