DGGS - Line Geometry

Differential Geometry and Geometric Structures

Main Page | Research Areas | Line Geometry

	Line Geometry We study differential geometric invariants of ruled surfaces, line congruences, and complexes of lines.
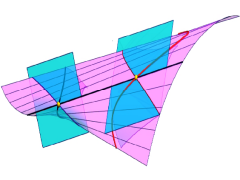
The two branches of the curve of flecnodes on a ruled surface and the intersection curves of the tangent planes at two flecnodes.	B. Odehnal: Note on flecnodes. J. Geom. Graphics 13/1 (2009), 29-40. The flecnodes F_i on a regular and non torsal ruling R₀ of a ruled surface R are the points where R's asymptotic tangents along R₀ hyperosculate the ruled surface. The name flecnode characterizes the intersection curve c_i of the tangent plane τ_i with R at F_i. It has a double point (a node) at F_i and this node is an inflection point for both linear branches of c_i at F_i. We show a way to parameterize the smooth one-parameter family of flecnodes of R which in general forms a curve with two branches. For that we derive the equation of the ruled quadric on three given lines in terms of Plücker coordinates of the given lines.
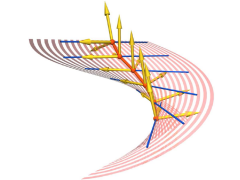
Reconstruction of a helical surface	B. Odehnal: Subdivision algorithms for ruled surfaces. J. Geom. Graphics 12/1 (2008), 35-52. Recent research has produced results on subdivision in arbitrary manifolds. These results can be applied to the manifold of lines and thus we can create subdivision schemes especially for ruled surfaces. We present different methods for refining discrete models of ruled surfaces: An algorithm combining subdivision and projection to the manifold of lines in Euclidean three-space. A further algorithm combines subdivision for the striction curve with geodesic subdivision in the Euclidean unit sphere. The third method is based on the Denavit-Hartenberg method for serial robots. We refine the sequence of motions of the Sannia frame by means of geodesic subdivision in the group of Euclidean motions.
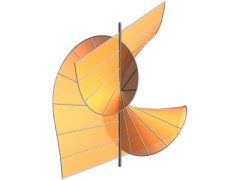
Cayley's ruled cubic surface	H. Havlicek: Cayley's surface revisited, J. Geom. 82 (2005), 71-82. Preprint (PDF) Cayley's ruled cubic surface (in the three-dimensional real projective space) carries a three-parameter family of twisted cubics. All of them share a common point U with a common tangent t, and a common osculating plane ω, say. The point U is a pinch point of the surface. (See the figure on the left hand side.) We describe the contact of higher order at U and the dual contact of higher order at ω for these curves and show that there are three exceptional cases. Reference: H. Brauner: Geometrie auf der Cayleyschen Fläche. Österreich. Akad. Wiss. Math.-Natur. Kl. S.-B. II 173 (1964), 93-128.
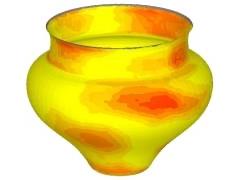
	H. Pottmann, M. Hofer, B. Odehnal, and J. Wallner. Line geometry for 3D shape understanding and reconstruction. In T. Pajdla and J. Matas, editors, Computer Vision - ECCV 2004, Part I, volume 3021 of Lecture Notes in Computer Science, pages 297-309. Springer, 2004. We understand and reconstruct special surfaces from 3D data with methods from line geometry. Based on estimated surface normals, we use approximation techniques in line space to recognise and reconstruct rotational, helical, developable, and other surfaces, which are characterised by the configuration of locally intersecting surface normals. For the computational solution we use a modified version of the Klein model of line space. Obvious applications of these methods lie in Reverse Engineering. We have tested our algorithms on real world data obtained from objects, such as antique pottery, gear wheels, and a surface of the ankle joint.

Publications

B. Odehnal and H. Pottmann. Computing with discrete models of ruled surfaces and line congruences. In F. C. Park and C. C. Iurascu, editors, Computational Kinematics, pages 211-226, 2001. Proceedings of the workshop in Seoul, May 19-22, 2001.
H. Pottmann and J. Wallner. Computational Line Geometry. Mathematics + Visualization. Springer, Heidelberg, 2001. ISBN 3-540-42058-4.
B. Odehnal and H. Stachel. The upper talocalcanean join. Technical Report 127, Geometry Preprint Series, Vienna Univ. of Technology, October 2004.
H. Pottmann, M. Hofer, B. Odehnal, and J. Wallner. Line geometry for 3D shape understanding and reconstruction. In T. Pajdla and J. Matas, editors, Computer Vision - ECCV 2004, Part I, volume 3021 of Lecture Notes in Computer Science, pages 297-309. Springer, 2004, ISBN 3-540-21984-6.
J. Gmainer and H. Havlicek: Isometries and collineations of the Cayley surface, Innov. Incidence Geom. 2 (2005), 109-127.
Preprint (PDF)
H. Havlicek: Higher order contact on Cayley's ruled cubic surface, In: G. Weiß (ed.): Proceedings - 30. Süddeutsches Kolloquium über Differentialgeometrie, Institut für Geometrie, TU Dresden, Dresden, 2005, pp. 27-34. (ISBN 3-86005-484-8)
Preprint (PDF)
H. Havlicek: Cayley's surface revisited, J. Geom. 82 (2005), 71-82.
Preprint (PDF)
M. Hofer, B. Odehnal, H. Pottmann, T. Steiner, and J. Wallner. 3D shape recognition and reconstruction based on line element geometry. In Tenth IEEE International Conference on Computer Vision, volume 2, pages 1532-1538. IEEE Computer Society, 2005, ISBN 0-7695-2334-X.
B. Odehnal: On isotropic congruences of lines in elliptic three-space. Math. Pannon. 16 (2005), 119-135.
B. Odehnal: On rational isotropic congruences of lines. J. Geom. 81 (2005), 126-138.
B. Odehnal: Über isotrope Geradenkongruenzen. In 30. Süddeutsches Differentialgeometrie-Kolloquium, pages 51-62. TU Dresden, 2005, ISBN 3-86005-484-8.
B. Odehnal, H. Pottmann, and J. Wallner: Equiform kinematics and the geometry of line elements. Beitr. Algebra Geom. 47/2 (2006), 567-582.
B. Odehnal: Subdivision algorithms for ruled surfaces. J. Geom. Graphics 12/1 (2008), 35-52.
H. Havlicek, F. Manhart, and B. Odehnal (eds.): Proceedings - 33. Süddeutsches Kolloquium über Differentialgeometrie, Institut für Diskrete Mathematik und Geometrie, TU Wien, Wien, 2008, iii + 89 pp, ISBN-13: 978-3-902233-04-2.
Link to full text