
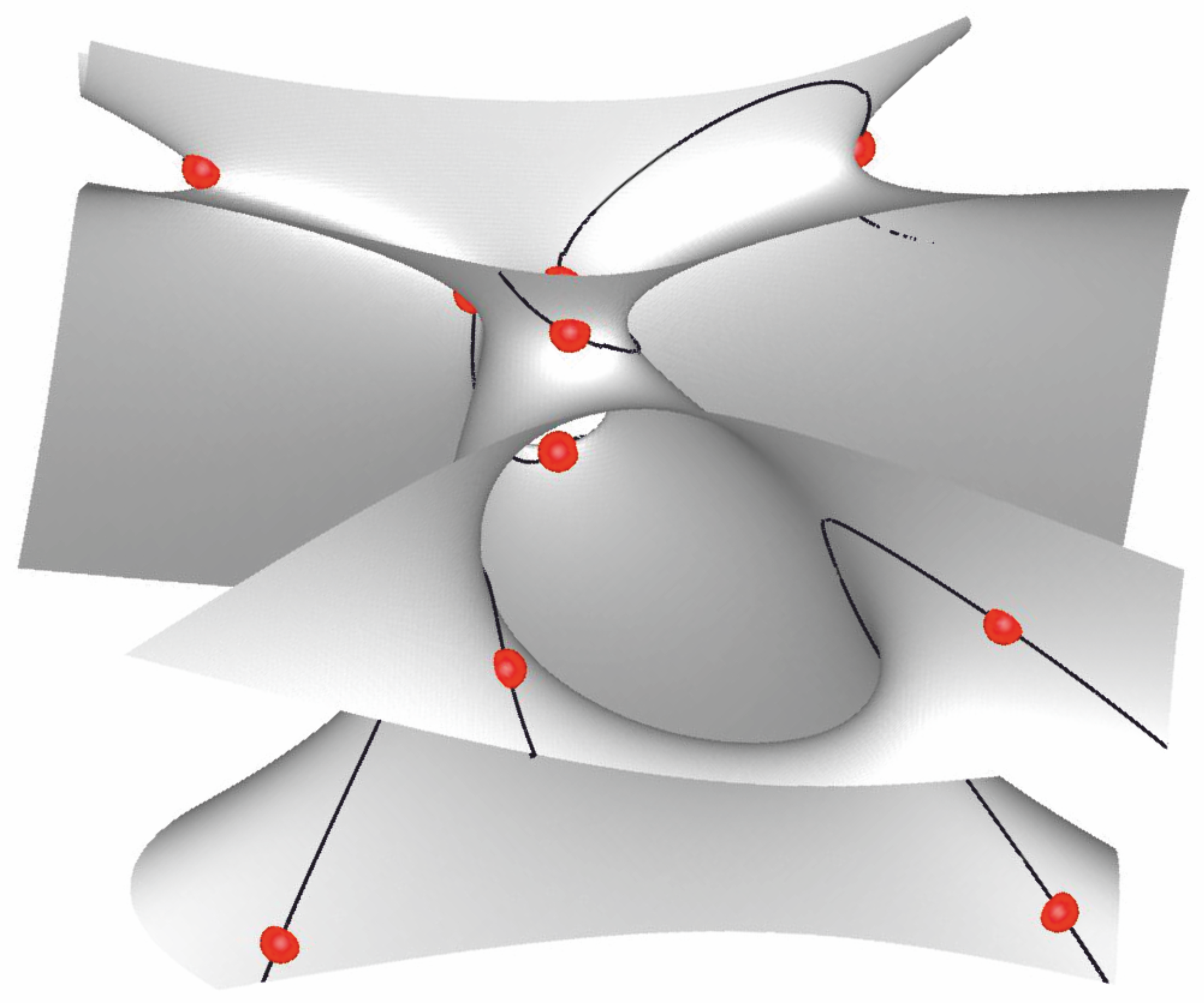
Configuration space of a 3-RPR manipulator:
Points of the surface (gray), curve (black), discrete set (red) correspond to configurations of flexion order 1, 2 and 3, respectively.
|
Higher-Order Flexibility of Geometric Structures
This project is devoted to the determination of flexes associated with higher-order flexible structures.
This project is funded by the Austrian Science Fund (FWF).
Grant DOI: 10.55776/PAT1144724
Duration: 2025-2029
FWF-Funding: € 223 849.88
Project leader: Georg Nawratil
Aims and Scope
The main goal of this FWF project on the crossroads of kinematics, algebraic geometry and rigidity theory is the determination of flexes associated with higher-order flexible structures using a global approach based on Puiseux series and tropical geometry. Moreover, it is planned to study generalizations of the averaging technique and to design/analyze examples with special properties regarding higher-order flexion, e.g. higher-order cusp mechanisms.
This basic research finds application in the promising field of model flexors, which have high practical potential ranging from robotics over origami to engineering applications in architecture.
Project Publications
-
G. Nawratil: On flexes associated with higher-order flexible bar-joint frameworks.
Advances in the Mathematics of Robotics (W. Holderbaum, J.M. Selig eds.), in press, Springer, 2026, DOI: 10.1007/978-3-032-10510-3_6
[arXiv:2502.01124]
-
F. Dellinger, M. Kilian, M. Lee, C. Müller, G. Nawratil, T. Tachi, K. Sharifmoghaddam:
Snapping Deployable Toroids for Modular Gridshells. ACM Transactions on Graphics 44(6):235 (2025)
[Preprint]
DOI 10.1145/3763808
Project Talks
-
G. Nawratil:
3rd
IMA Conference on Mathematics of Robotics, Manchester September 24-26 2025, United Kingdom, paper presentation.
|

 Technische Universität Wien
Technische Universität Wien
