
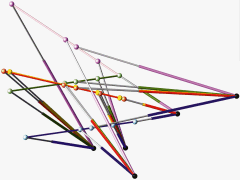
Given is a non-singular pose (green) of a pentapod with linear platform and non-planar base (black anchor points).
The closest singular configuration in the position/orientation workspace is illustrated in blue/magenta.
The closest singular pose under Euclidean/equiform motions of the linear platform is displayed in red/yellow.
|
Singularity Closeness of Stewart-Gough Platforms
This project is devoted to evaluating the closeness of Stewart-Gough platforms to singularities.
This project is funded by the Austrian Science Fund (FWF).
FWF grant no. P 30855-N32
Duration: 2018-2022
FWF-Funding: € 192 774.76
Project leader: Georg Nawratil
Aims and Scope
A parallel manipulator of Stewart-Gough (SG) type consists of a moving platform, which is connected via spherical-prismatic-spherical legs with the base,
where only the prismatic joints are active. The number of applications of SG manipulators, ranging from medical surgery to astronomy,
has increased enormously during the last decades due to their advantages of high speed, stiffness, accuracy, load/weight ratio, etc.
One of the drawbacks of these parallel robots are their singular configurations, where the manipulator is shaky while all leg lengths are fixed.
As a consequence the actuator forces can become very large, which may result in a breakdown of the mechanism.
Therefore singularities have to be avoided. This reasons the high interest of the kinematic/robotic community in evaluating the singularity closeness of SG platforms,
but geometric meaningful distance measures for this task are still missing. The research project closes this gap.
Project Publications
-
G. Nawratil:
Singularity Distance for Parallel Manipulators of Stewart Gough Type.
Advances in Mechanism and Machine Science –
Proc. of the 15th IFToMM World Congress on Mechanism and Machine Science (T. Uhl ed.), pages 259-268, Springer, 2019, ISBN 978-3-030-20131-9,
DOI 10.1007/978-3-030-20131-9_26
[Preprint]
-
A. Rasoulzadeh and G. Nawratil:
Variational Path Optimization of Linear Pentapods with a Simple Singularity Variety.
Mechanism and Machine Theory 153 (12) 104002 (2020) DOI 10.1016/j.mechmachtheory.2020.104002
[arXiv:1910.04810]
Supplementary data:
see homepage of Arvin Rasoulzadeh
-
G. Nawratil:
Evaluating the snappability of bar-joint frameworks.
Advances in Robot Kinematics (J. Lenarcic, B. Siciliano eds.), pages 182-189, Springer, 2020, ISBN 978-3-030-50974-3,
DOI 10.1007/978-3-030-50975-0_23
[Extended version on arXiv:2001.04430]
Supplementary data:
Animations of the snapping deformation of Fig. 2:
left,
center,
right
-
A. Kapilavai and G. Nawratil: On homotopy continuation based singularity distance computations for 3-RPR manipulators.
New Trends in Mechanism Science (D. Pisla, B. Corves eds.), pages 56-64, Springer, 2020, ISBN 978-3-030-55060-8,
DOI 10.1007/978-3-030-55061-5_8
[Extended version on arXiv:2004.08359]
-
G. Nawratil:
On the snappability and singularity-distance of frameworks with bars and triangular plates.
In Proceedings of
2nd
IMA Conference on Mathematics of Robotics (W. Holderbaum, J.M. Selig eds.), pages 144-152, Springer, 2022, ISBN 978-3-030-91351-9,
DOI 10.1007/978-3-030-91352-6_15
[arXiv:2003.09904]
-
A. Kapilavai, G. Nawratil: Metrics for distance computation between 3-RPR configurations.
Extended Abstract published in Proc. of 7. IFToMM D-A-CH Konferenz,
February 18-19 2021, online conference due to COVID-19, DOI 10.17185/duepublico/74051
-
G. Nawratil:
Snappability and singularity-distance of pin-jointed body-bar frameworks.
Mechanism and Machine Theory 167 104510 (2022) DOI 10.1016/j.mechmachtheory.2021.104510
[arXiv:2101.02490]
Supplementary data:
Animations of the snapping of
Example 2, the
Siamese dipyramid and the
Four-horn as well as the
expression of the shakiness factor S for the Siamese dipyramid and
the Four-horn, respectively
-
G. Nawratil:
On origami-like quasi-mechanisms with an antiprismatic skeleton.
Advances in Robot Kinematics 2022 (O. Altuzarra, A. Kecskemethy eds.), pages 13-21, Springer, 2022, ISBN 978-3-031-08139-2, DOI 10.1007/978-3-031-08140-8_2
[Extended version on arXiv:2108.01950]
Supplementary data:
Animations of snapping sandglass polyhedra for n=3,
4,
5,
6
and shaky sandglass polyhedra for n=3,
4,
5,
6
-
G. Nawratil:
Multi-stable design of triangulated origami structures on cones of revolution.
Computer Aided Geometric Design 95 102105 (2022)
DOI 10.1016/j.cagd.2022.102105
[arXiv:2110.10986]
-
G. Nawratil:
Origami-like quasi-mechanisms with an antiprismatic skeleton.
Mechanism and Machine Theory 181 105214 (2023)
DOI 10.1016/j.mechmachtheory.2022.105214
[Open Access]
Supplementary data:
Animations of snapping sandglass polyhedra for n=3,
4,
5,
6
and shaky sandglass polyhedra for n=3,
4,
5,
6
-
A. Kapilavai, G. Nawratil: Singularity Distance Computations for 3-RPR Manipulators using Extrinsic Metrics. Mechanism and Machine Theory 195 105595 (2024)
DOI 10.1016/j.mechmachtheory.2024.105595
[Open Access]
-
A. Kapilavai, G. Nawratil: Singularity Distance Computations for 3-RPR Manipulators using Intrinsic Metrics. Computer Aided Geometric Design
111 102343 (2024) DOI 10.1016/j.cagd.2024.102343
[Open Access]
-
A. Kapilavai, G. Nawratil: Architecture Singularity Distance Computations for Linear Pentapods.
ASME Journal of Mechanisms Robotics 17 (2) 021008 (2025)
DOI 10.1115/1.4065789
[arXiv:2312.09160]
Project Talks
-
G. Nawratil:
15th IFToMM World Congress,
Krakow June 30-July 4 2019, Poland, paper presentation.
[Slides]
-
G. Nawratil:
SIAM Conference on Applied Algebraic Geometry,
Bern July 9-13 2019, Switzerland, Invited Talk (Mini-symposium: Algebraic geometry for kinematics, mechanism science, and rigidity),
Title: Singularity distance computation for parallel manipulators of Stewart Gough Type.
[Slides]
-
G. Nawratil:
Workshop on Circle Packings and Geometric Rigidity,
July 6-10 2020, online due to COVID-19 hosted by ICERM,
Lightning Talk,
Title: On the snappability of frameworks. [Slides]
-
A. Kapilavai:
PARALLEL 2020, The 4th International Workshop on Fundamental Issues,
Applications and Future Research Directions for Parallel Mechanisms/Manipulators/Machines,
September 9-11 2020, online conference due to COVID-19, Title: On homotopy continuation based singularity distance computations for 3-RPR manipulators.
[Slides]
-
G. Nawratil:
TUForMath, TU Wien December 3 2020, Austria, Public Talk (in German) held online due to COVID-19, Title: Forme(l)n der Beweglichkeit.
[Talk on YouTube,
Slides]
-
A. Kapilavai:
7. IFToMM D-A-CH Konferenz,
February 18-19 2021, online conference due to COVID-19, Title: Metrics for distance computation between 3-RPR configurations.
-
A. Kapilavai:
Effective Methods in Algebraic Geometry (MEGA 2021),
June 7-11 2021, oral presentation in the software session held online due to COVID-19, Title: Algorithms for distance computations between 3-RPR configurations.
-
G. Nawratil:
Workshop on Real Algebraic Geometry and
Algorithms for Geometric Constraint Systems, June 14-18 2021, online due to COVID-19 hosted by the Fields Institute, Title:
Snappability and singularity-distance of frameworks.
[Talk on YouTube,
Slides]
-
G. Nawratil:
2nd
IMA Conference on Mathematics of Robotics, September 8-10 2021, online due to COVID-19 hosted by IMA, paper presentation.
[Slides]
-
G. Nawratil:
Conference on Geometry: Theory and Applications, Gozd Martuljek September 20-23 2021, Slovenia, Title:
Multistable Design of Triangulated Cones.
[Abstract,
Slides]
-
A. Kapilavai:
ICRA 2022 Workshop "New Frontiers of Parallel Robotics",
Philadelphia May 27 2022, USA, oral online-presentation in the session "my work in 5 minutes" held hybrid due to COVID-19,
Title: Architecture Singularity Distance Computations for Linear Pentapods.
-
G. Nawratil:
18th International Symposium on Advances in Robot Kinematics (ARK'22), Bilbao June 26-30 2022, Spain, paper presentation.
[Slides]
-
A. Kapilavai:
Conference on Geometry: Theory and Applications, Kefermarkt June 19-23 2023, Austria, Title:
Singularity Distance Computation for Parallel Manipulators of Stewart-Gough Type.
[Abstract]
|

 Technische Universität Wien
Technische Universität Wien
