Differential Geometry and Geometric Structures

Main Page | Research Areas | Spreads and Parallelisms

Spreads and Parallelisms

The topic of our research are connections among spreads and parallelisms of projective spaces with areas like the geometry of field extensions, topological geometry, translation planes or flocks of quadrics.

Spreads

A spread in a three-dimensional projective space is a set of lines such that each point of the space is incident with exactly one line. Each spread gives rise to a translation plane, i.e., a special type of a projective plane.

Of special interest are examples of topological translation planes and their automorphism groups, where, for instance, classical line geometry is used in order to construct examples of spreads.

Regular spread

Regular Spreads

A classical example of a spread is an elliptic linear congruence of lines or, in other words, a regular spread.

In the picture on the left some lines of such a spread in the real 3-space are shown. This spread arises as follows:

First, take two parallel planes (the brown disks) and a line (the white axis) perpendicular to both planes. Through each point of the lower disk there is a line parallel to the axis. Those lines are made out of rubber strings.

Next, the upper disk is rotated around the white axis through some angle less than 180 degrees. Now the stretched rubber strings form a regular spread. We add, for the sake of completeness, that the common line at infinity of the two disks belongs also to the spread.

In the present model a polar coordinate system has been drawn in the lower plane and only some of the spread's lines have been materialised.

Observe that the lines of the spread along each of the circles drawn in the lower plane form a regulus which is lying on a hyperboloid of revolution of one sheet. The lines of the spread along the radial lines form reguli too. Each of those reguli is on a hyperbolic paraboloid.

The translation plane arising from this spread is the complex projective plane.

A spread of Betten

A Topological Spread of D. Betten

The second example of a spread arises from the model above by replacing the radial lines in the upper disk by certain curves and changing the rubber strings accordingly. The lower disk remains unchanged. Also, the angle of revolution is subject to stronger restrictions than before. The actual details of the construction are too involved to be written down here.

The corresponding translation plane has been discovered by Dieter Betten (University of Kiel, Germany) by a different approach in the year 1970. This plane is a four-dimensional topological manifold. Moreover, it is non-desarguesian, so that it cannot be coordinatised by a skew field. Since we have a translation plane, it is possible however, to introduce coordinates coming from a quasifield.

Comparison

A Comparison of Models

On our next picture you can see once more the essential difference between the two models from the above, namely the radial curves and the radial lines on the upper disks, respectively. Recall that the lower disks (invisible on the photograph) are identical in both models.

Thus it is possible to see, how the complex projective plane turns into a (non-desarguesian) translation plane.

Also on the picture is our dear friend Rolf Riesinger, a former staff member of the institute.

It was him who built with great passion all the marvellous models presented on this page.

Piecewise regular spread

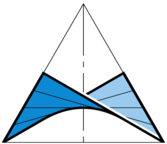
A Piecewise Regular Spread

We proceed by presenting a model of a topological spread of the three-dimensional real projective space which arises by gluing together two pieces of regular spreads (with strings in yellow and blue, respectively) along a common regulus (in green).

More generally, several pieces of regular spreads may be glued together along common reguli to obtain explicit examples of topological spreads which are rigid or even hyperrigid.

Rigidity of a spread means that it admits no collineation other than the identity. A rigid spread is said to be hyperrigid if it does not admit any correlation.

A rigid spread need not be hyperrigid, even if it is topological.

Detail

The final picture shows the model from above in detail.

The corresponding 4-dimensional non-desarguesian translation plane is also due to Dieter Betten. He established its existence in the year 1972.

Publications

H. Havlicek: Dual spreads generated by collineations, Simon Stevin 64 (1990), 339-349.
Preprint (PDF)
R. Riesinger: Beispiele starrer topologischer Faserungen des reellen projektiven 3-Raums, Geom. Dedicata 40 (1991), 145-163.
R. Riesinger: Faserungen, die aus Reguli mit einem gemeinsamen Geradenpaar zusammengesetzt sind, J. Geom. 45 (1992), 137-157.
R. Riesinger: Faserungen, die aus Reguli mit gemeinsamer Berührprojektivität längs einer gemeinsamen Erzeugenden zusammengesetzt sind, Geom. Dedicata 44 (1992), 295-312.
H. Havlicek: On the geometry of field extensions, Aequat. math.45 (1993), 232-238.
Preprint (PDF)
H. Havlicek: Baer subspaces within Segre manifolds, Result. Math. 23 (1993), 322-329.
Preprint (PDF)
H. Havlicek: Spreads of right quadratic skew field extension, Geom. Dedicata 49 (1994), 239-251.
Preprint (PDF)
R. Riesinger: Spreads admitting net-generating regulizations, Geom. Dedicata 62 (1996), 139-155.
R. Riesinger: Spreads admitting elliptic regulizations, J. Geom. 60 (1997), 127-145.
H. Havlicek: Affine circle geometry over quaternion skew fields, Discrete Math. 174 (1997), 153-165.
Preprint (PDF)
R. Riesinger: Extending the Thas-Walker construction, Bull. Belg. Math. Soc. Simon Stevin 6 (1999), 237-247.
A. Blunck: Regular spreads and chain geometries, Bull. Belg. Math. Soc. Simon Stevin 6 (1999), 589-603.
A. Blunck and H. Havlicek: Affine spaces within projective spaces, Result. Math. 36 (1999), 237-251.
Preprint (PDF)
R. Riesinger: The second extension of the Thas-Walker construction, Beitr. Algebra Geometrie 41 (2000), 479-488.
D. Betten, R. Riesinger: Discussing Knarr's 2-surface of R⁴ which generates the first single shift plane, Geom. Dedicata 83 (2000), 329-342.
R. Riesinger: A class of topological spreads with unisymplecticly complemented regulization, Results Math. 38 (2000), 307-338.
D. Betten, R. Riesinger: Noncommutative line spaces derived from certain ovals of 4-dimensional translation planes, Publ. Math. Debrecen 62 (2003), 117-130.
R. Riesinger: Piecewise regular spreads, Results Math. 45 (2004), 153-168.
R. Riesinger: Constructing non-regular algebraic spreads with asymplecticly complemented regulization, Beitr. Algebra Geometrie 46 (2005), 179-206.
D. Betten, R. Riesinger: Topological parallelisms of the real projective 3-space, Results Math. 47 (2005), 226-241.
H. Havlicek and R. Riesinger: The Betten-Walker spread and Cayley's ruled cubic surface, Unserem lieben Freund Dieter Betten zum 65. Geburtstag gewidmet, Beitr. Algebra Geom. 47 (2006), 527-541.
Preprint (PDF)
D. Betten and R. Riesinger: Constructing topological parallelisms of PG(3,ℝ) via rotation of generalized line pencils, Adv. Geom. 8 (2008), 11-32.
D. Betten and R. Riesinger: Generalized line stars and topological parallelisms of the real projective 3-space, J. Geom. 91 (2009), 1-20.
D. Betten and R. Riesinger: Hyperflock determining line sets and totally regular parallelisms of PG(3,ℝ), Monatsh. Math. 161 (2010), 43-58.
D. Betten and R. Riesinger: Parallelisms of PG(3,ℝ) composed of non-regular spreads, Aequationes Math. 81 (2011), 227-250.
D. Betten and R. Riesinger: Clifford parallelism: old and new definitions, and their use, J. Geom. 103 (2012), 31-73.
D. Betten and R. Riesinger: Collineation groups of topological parallelisms, Adv. Geom. 14 (2014), 175-189.
D. Betten and R. Riesinger: Automorphisms of some topological regular parallelisms of PG(3,ℝ), Results Math. 66 (2014), 291-326.
D. Betten and R. Riesinger: Regular 3-dimensional parallelisms of PG(3,ℝ), Bull. Belg. Math. Soc. Simon Stevin 22 (2015), 813-835.
H. Havlicek: A note on Clifford parallelisms in characteristic two, Publ. Math. Debrecen 86/1-2 (2015), 119-134.
DOI: 10.5486/PMD.2015.7034
Preprint (PDF) | Article (external link)
H. Havlicek: Clifford parallelisms and external planes to the Klein quadric, J. Geom. 107 (2016), 287-303.
DOI: 10.1007/s00022-015-0303-1
Preprint (PDF) | Article (external link)
H. Havlicek and R. Riesinger: Pencilled regular parallelisms, In memoriam Walter Benz, Acta Math. Hungar. 153 (2017), 249-264.
DOI: 10.1007/s10474-017-0742-2
Preprint (PDF) | Article (external link)
H. Havlicek, S. Pasotti and S. Pianta: Clifford-like parallelisms, Dedicated to Helmut Karzel on the occasion of his 90th birthday, J. Geom. 110 (2019), Art. 2.
DOI: 10.1007/s00022-018-0456-9
Preprint (PDF) | Article (external link, open access)
H. Havlicek, S. Pasotti and S. Pianta: Automorphisms of a Clifford-like parallelism, Adv. Geom. 21 (2021), 63-73.
DOI: 10.1515/advgeom-2020-0027
Preprint (PDF) | Article (external link)
H. Havlicek, S. Pasotti and S. Pianta: Characterising Clifford parallelisms among Clifford-like parallelisms, Dedicated to Mario Marchi on the occasion of his 80th birthday, in friendship, Beiträge Algebra Geom.62 (2021), 37-54.
DOI: 10.1007/s13366-020-00509-4
Preprint (PDF)

Quick Links

Andrea Blunck

Hans Havlicek

A Tribute to Rolf Riesinger (1945-2018)

Chain Geometry

Grassmann Spaces

Line Geometry

Sitemap

External Links

Silvia Pianta, Catholic University of Brescia

Stefano Pasotti, University of Brescia