|
Geometry of Mechanisms
We are interested in flexible and in infinitesimally flexible structures - in theory as well as in applications, like gearing or the design of mechanisms for real world problems.
|
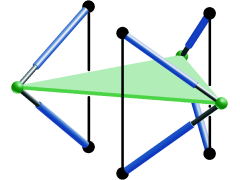
Figure 1: Non-planar manipulator with cylindrical singularity surface.
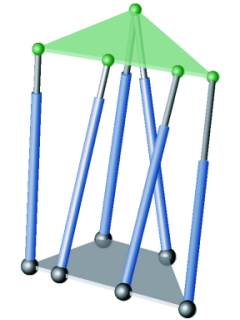
Figure 2: Planar manipulator (type II) with cylindrical singularity surface.
|
G. Nawratil: Results on Planar Parallel Manipulators with Cylindrical Singularity Surface. Advances in Robot Kinematics - Analysis and Design (J. Lenarcic, P. Wenger eds.), pages 321-330, Springer, 2008, ISBN 978-1-4020-8599-4.
G. Nawratil: Main Theorem on Planar Parallel Manipulators with Cylindrical Singularity Surface. In Proc. of 33rd South German Colloquium on Differential Geometry, TU Vienna, to appear.
G. Nawratil:
All Planar Parallel Manipulators with Cylindrical Singularity Surface. Technical Report No. 191, Geometry Preprint Series, Vienna Univ. of Technology, August 2008.
There are only two types of non-architecturally singular parallel manipulators (of Stewart Gough type) with planar base and platform, whose singularity set for any orientation of the platform is a cylindrical surface with rulings parallel to a given fixed direction p in the space of translations.
These manipulators have the advantage that their singularity set can easily be visualised as conic section by choosing p as projection direction. Moreover the computation of singularity free zones reduces to a 5-dimensional task.
Furthermore, we conjecture that there exists only one such design (see Figure 1) for the non-planar case, namely the generalisation of type I of the planar case.
An example for type II of the planar case is illustrated in Figure 2.
|
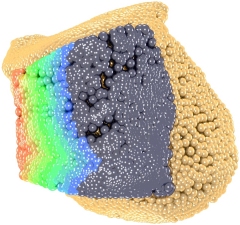
Contact areas of the facies articulatio trochlea talii superior and the facies articulatio tibiae inferior.
|
B. Odehnal and H. Stachel. The upper talocalcanean join. Technical Report 127, Geometry Preprint Series, Vienna Univ. of Technology, October 2004.
We reconstruct special surfaces like rotational and helical ones from 3D data with line geometry methods. This technique is applied to the surface of the talocalcanean join in order to understand in what sense the geometry of the surface influences the motion of body parts.
|
|
|
Publications
-
H. Stachel.
A family of multiply decomposable Euclidean motions.
In I. Bárány and K. Böröcky, editors, Intuitive geometry
(Budapest, 1995), volume 6 of Bolyai Soc. Math. Stud., pages
413-427. János Bolyai Math. Soc., Budapest, 1997, ISBN 963-8022-89-2.
Proceedings of the 5th conference, Budapest 1995.
[Zbl], [MR].
-
H. Stachel.
Computer animation, a tool for the design of
mechanisms.
In B. Kovács and Z. Kovács, editors, International Conference on
Applied Informatics, pages 127-139, 1995.
held in Eger, Hungary, August 23--25, 1995.
-
H. Stachel.
A remarkable overconstrained spherical
motion.
In J. Lenarčič and M. Husty, editors, Advances in robot
kinematics: analysis and control (Salzburg, 1998), pages 287-296. Kluwer
Acad. Publ., Dordrecht, 1998, ISBN 0-7923-5169-X.
[Zbl], [MR].
-
H. Stachel.
Higher-order flexibility for a bipartite
planar framework.
In A. Kecskeméthy, M. Schneider, and C. Woernle, editors, Advances in
Multibody Systems and Mechatronics, pages 345-357. Inst. f. Mechanik
und Getriebelehre, TU Graz, Duisburg, 1999, ISBN 3-9501108-0-1.
-
H. Stachel.
Infinitesimal flexibility of higher order for
a planar parallel manipulator.
In G. Karáné, H. Sachs, and F. Schipp, editors, Topics in Algebra,
Analysis and Geometry, pages 343-353. BPR Kiadó, 1999, ISBN
963-03-8502-3.
Proceedings of the Gyula Strommer national memorial conference,
Balatonfüred, Hungary, May 1--5, 1999.
[Zbl].
-
H. Stachel.
Higher order flexibility of octahedra.
Period. Math. Hungar. 39 (1999), 225-240, Discrete geometry and
rigidity (Budapest, 1999).
[Zbl], [MR].
-
Vorrichtung zum Nadeln eines Vlieses.
Patentschrift AT 408 234 B, Republik Österreich.
-
H. Stachel.
Das Gleichlauf-Kugelgelenk - ein
Beispiel zum anwendungsorientierten Unterricht aus Darstellende
Geometrie.
In SDG Symposium Darstellende Geometrie, pages 151-156. TU Dresden,
Institut für Geometrie, 2000, ISBN 3-86005-258-6.
Proceedings of the conference held June 15.-17, 2000.
-
H. Stachel.
Instantaneous spatial kinematics and the
invariants of the axodes.
In Proceedings Ball 2000 Symposium, Cambridge, 2000.
No. 23, 14 p.
-
H. Stachel.
Configuration theorems on bipartite
frameworks.
Rend. Circ. Mat. Palermo (2) Suppl. 70/II (2002), 335-351, IV
International Conference in Stochastic Geometry, Convex Bodies, Empirical
Measures & Applications to Engineering Science, Vol. II (Tropea, 2001).
[MR].
-
H. Stachel.
Schraubtorsen als Zahnflanken.
Inf. Bl. Darst. Geom. 23/2 (2004), 46-50.
-
B. Odehnal and H. Stachel.
The upper talocalcanean join.
Technical Report 127, Geometry Preprint Series, Vienna Univ. of Technology,
October 2004.
-
H. Stachel.
On Jack Phillips' spatial involute
gearing.
In Y. Zuo et al., editors, The 11th International Conference on Geometry
and Graphics, pages 43-48. Stankin/Yanus-K., Moscow, 2004, ISBN
5-8037-0184-X.
held in Guangzhou, China, August 1-5, 2004.
-
H. Stachel.
Teaching spatial kinematics for engineers.
Internat. Conference on Engineering Education 2005/2, 845-851,
Jerzy Mościński and Marcin Maciażek, eds.
-
H. Stachel.
On spatial involute gearing.
In L. Csöke et al., editors, Proc. 6th ICAI, Eger/Hungary, January
27-31, volume 1, pages 27-40. 2005.
-
G. Nawratil.
New
performance indices for 6R robot postures.
In M. Husty and H.-P. Schröcker, editors, Proceedings of EuCoMeS,
2006, ISBN 3-901249-85-0.
12pp. held in Obergurgl, Feb. 21--26, 2006 [electronic].
-
G. Nawratil.
The control
number as index for Stewart-Gough platforms.
In J. Lenarčič and B. Roth, editors, Advances in Robot Kinematics, Mechanisms and Motion, pages 15-22. Springer, 2006, ISBN 1-4020-4940-4.
-
G. Figliolini, H. Stachel, J. Angeles.
A new look at the Ball-Disteli diagram and its
relevance to spatial gearing.
Mech. Mach. Theory 42/10 (2007), 1362-1375.
-
G. Nawratil. New Performance Indices for 6R Robots. Mechanism and Machine Theory 42 (11), 1499-1511 (2007).
-
G. Nawratil: New Performance Indices for 6-dof UPS and 3-dof RPR Parallel Manipulators. Mechanism and Machine Theory, to appear.
-
G. Nawratil: Results on Planar Parallel Manipulators with Cylindrical Singularity Surface. Advances in Robot Kinematics - Analysis and Design (J. Lenarcic, P. Wenger eds.), pages 321-330, Springer, 2008, ISBN 978-1-4020-8599-4.
-
G. Nawratil: Main Theorem on Planar Parallel Manipulators with Cylindrical Singularity Surface. In Proc. of 33rd South German Colloquium on Differential Geometry, TU Vienna, to appear.
-
G. Nawratil: Comments on "Architecturally singular non-planar parallel manipulators". Technical Report No. 188, Geometry Preprint Series, Vienna Univ. of Technology, May 2008.
-
G. Nawratil:
All Planar Parallel Manipulators with Cylindrical Singularity Surface. Technical Report No. 191, Geometry Preprint Series, Vienna Univ. of Technology, August 2008.
|
|
Quick Links
Georg Nawratil
Boris Odehnal
Hellmuth Stachel
Flexible Structures
Higher-Order Flexibility of Geometric Structures
Line Geometry
Stewart Gough Platforms with Self-Motions
Singularity Closeness of Stewart-Gough Platforms
Analyse ebener Getriebe
(in German)
Sitemap
|

 Technische Universität Wien
Technische Universität Wien
