
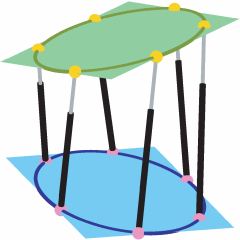
Due to a result from M. Chasles (1861) it is known, that planar SGPs, where the platform anchor points and corresponding base anchor points are
related by a non-singular projectivity, are architecturally singular, if the anchor points are located on a conic.
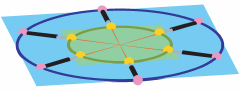
Moreover, it is known that all architecturally singular SGPs are redundant. Therefore, they possess a self-motion in each pose.
It can easily be seen by the above given example, that this only holds over the complex number field. In the given pose the platform and the base
coincide as well as the centers of the two circles (projectivity is a similarity).
|
Stewart Gough Platforms with Self-Motions
The main aim of the project is the systematic determination, investigation and classification of Stewart Gough platforms with self-motions.
This project is funded by the Austrian Science Fund (FWF).
FWF grant no. P 24927-N25
Duration: 2013-2018 (extended for 24 months without additional costs)
FWF-Funding: € 319 347.00
Project leader: Georg Nawratil
Aims and Scope
A Stewart Gough platform (SGP) is a parallel manipulator, consisting of a moving platform, which is connected via six spherical-prismatic-spherical legs with the base,
where only the prismatic joints are active. If the geometry of the SGP and the six leg lengths are given, then the manipulator is in general rigid, but under particular conditions
it can perform an n-parametric motion (n>0), which is called self-motion.
Moreover, all self-motions are solutions to the still unsolved problem posed by the French Academy of Science for the Prix Vaillant of the year 1904,
which is also known as Borel Bricard problem and reads as follows: "Determine and study all displacements of a rigid body in which distinct points of the body move on spherical paths."
Project Publications
-
G. Nawratil: Correcting Duporcq's theorem.
Mechanism and Machine Theory 73 282–295 (2014) DOI 10.1016/j.mechmachtheory.2013.11.012
[Open Access]
-
G. Nawratil: Introducing the theory of bonds for Stewart Gough platforms with self-motions.
ASME Journal of Mechanisms and Robotics 6 (1) 011004 (2014) DOI 10.1115/1.4025623
[Preprint]
-
G. Nawratil: On Stewart Gough manipulators with multidimensional self-motions.
Computer Aided Geometric Design 31 (7-8) 582-594 (2014) DOI 10.1016/j.cagd.2014.02.012
[Corresponding Technical Report]
-
G. Nawratil: Congruent Stewart Gough platforms with non-translational self-motions.
Proc. of 16th International Conference on Geometry and Graphics (H.-P. Schröcker, M. Husty eds.), Innsbruck, August 4-8 2014, Austria, pages 204-215, ISBN 978-3-902936-46-2
[Preprint]
Supplementary data: Exemplary self-motions, Animation
1a,
1b,
1c,
2a,
2b,
2c,
3a,
3b,
3c,
4a,
4b,
4c,
5a,
5b,
5c
-
G. Nawratil: On equiform Stewart Gough platforms with self-motions.
Journal for Geometry and Graphics 17 (2) 163-175 (2013)
[Preprint]
Supplementary data: Exemplary self-motions, Animation
1a,
1b,
1c,
2a,
2b,
2c,
3a,
3b,
3c
-
G. Nawratil: Kinematic Mapping of SE(4) and the Hypersphere Condition.
Advances in Robot Kinematics (J. Lenarcic, O. Khatib eds.), pages 11-19, Springer, 2014, ISBN 978-3-319-06697-4,
DOI 10.1007/978-3-319-06698-1_2
[Open Access,
Erratum]
-
M. Gallet, G. Nawratil and J. Schicho:
Bond theory for pentapods and hexapods. Journal of Geometry 106 (2) 211-228 (2015)
DOI 10.1007/s00022-014-0243-1
[arXiv:1404.2149]
-
M. Gallet, G. Nawratil and J. Schicho:
Möbius Photogrammetry. Journal of Geometry 106 (3) 421-439 (2015)
DOI 10.1007/s00022-014-0255-x
[arXiv:1408.6716]
Erratum: Journal of Geometry 106 (3) 441-442 (2015) DOI 10.1007/s00022-015-0297-8
-
G. Nawratil and J. Schicho:
Pentapods with Mobility 2. ASME Journal of Mechanisms and Robotics 7 (3) 031016 (2015)
DOI 10.1115/1.4028934
[arXiv:1406.0647]
Supplementary data: Maple 17 Worksheets of the General Case
[mws,
pdf]
and the Special Case
[mws,
pdf]
discussed in the Appendix
-
G. Nawratil and J. Schicho:
Self-motions of pentapods with linear platform. Robotica 35 (4) 832-860 (2017) DOI 10.1017/S0263574715000843
[arXiv:1407.6126]
Supplementary data: Animations of
Example 1 and
Example 2
-
G. Nawratil:
On the Self-Mobility of Point-Symmetric Hexapods. In special issue
Rigidity and Symmetry (B. Schulze ed.),
Symmetry 6 (4) 954-974 (2014) DOI 10.3390/sym6040954
[Open Access]
-
G. Nawratil:
Fundamentals of quaternionic kinematics in Euclidean 4-space.
Advances in Applied Clifford Algebras 26 (2) 693-717 (2016) DOI 10.1007/s00006-015-0613-2
[Full-text View-only Version,
Corresponding Technical Report]
-
G. Nawratil:
Quaternionic approach to equiform kinematics and line-elements of Euclidean 4-space and 3-space.
Computer Aided Geometric Design 47 150-162 (2016) DOI 10.1016/j.cagd.2016.06.003
[Preprint]
-
M. Gallet, G. Nawratil and J. Schicho:
Liaison Linkages. Journal of Symbolic Computation 79 (1) 65-98 (2017) DOI 10.1016/j.jsc.2016.08.006
[arXiv:1510.01127]
Supplementary data:
Animation of the given Example and
Maple Worksheets of the proofs of Proposition 3.1
[mws,
pdf]
and Proposition 3.2
[mws,
pdf]
-
G. Nawratil:
On the line-symmetry of self-motions of linear pentapods.
Advances in Robot Kinematics 2016 (J. Lenarcic, J.-P. Merlet eds.), pages 149-159, Springer, 2017, ISBN 978-3-319-56801-0,
DOI 978-3-319-56802-7_16
[HAL version,
Extended version on arXiv:1510.03567]
Supplementary data: Maple Worksheet of the example given in the Appendix of the extended version
[mws,
pdf]
-
B. Aigner and G. Nawratil:
Planar Stewart Gough platforms with quadratic singularity surface.
New Trends in Mechanisms Science – Theory and Industrial Applications (P. Wenger, P. Flores eds.),
pages 93-102, Springer, 2016, ISBN 978-3-319-44155-9,
DOI 10.1007/978-3-319-44156-6_10
[Corresponding Technical Report]
-
G. Nawratil and J. Schicho:
Duporcq Pentapods. ASME Journal of Mechanisms and Robotics 9 (1) 011001 (2017)
DOI 10.1115/1.4035085
[Corresponding arXiv paper]
-
M. Gallet, G. Nawratil, J. Schicho and J.M. Selig:
Mobile Icosapods. Advances in Applied Mathematics 88 1-25 (2017) DOI 10.1016/j.aam.2016.12.002
[arXiv:1603.07304]
Supplementary data:
Animation of the given example and
Maple code
for generating statistical data on the number of real legs
-
G. Nawratil:
Point-models for the set of oriented line-elements – a survey.
Mechanism and Machine Theory 111 118-134 (2017)
DOI 10.1016/j.mechmachtheory.2017.01.008 [Preprint]
-
G. Nawratil:
Parallel manipulators in terms of dual Cayley-Klein parameters.
Computational Kinematics (S. Zeghloul et al. eds.), pages 265-273, Springer, 2017, ISBN 978-3-319-60866-2,
DOI 978-3-319-60867-9_30
[Preprint]
-
A. Rasoulzadeh and G. Nawratil:
Rational Parametrization of Linear Pentapod's Singularity Variety and the Distance to it.
Computational Kinematics (S. Zeghloul et al. eds.), pages 516-524, Springer, 2017, ISBN 978-3-319-60866-2,
DOI 978-3-319-60867-9_59
[Extended version on arXiv:1701.09107]
-
G. Nawratil and A. Rasoulzadeh:
Kinematically Redundant Octahedral Motion Platform for Virtual Reality Simulations.
New Advances in Mechanism and Machine Science (I. Doroftei et al. eds.),
pages 387-400, Springer, 2018, ISBN 978-3-319-79110-4, DOI 10.1007/978-3-319-79111-1_39
[arXiv:1704.04677]
Supplementary data:
Animation of the example given in Fig. 3
-
G. Nawratil:
Kinematic interpretation of the Study quadric's ambient space.
Advances in Robot Kinematics 2018 (J. Lenarcic, V. Parenti-Castelli eds.),
pages 3-11, Springer, 2019, ISBN 978-3-319-93187-6, DOI 10.1007/978-3-319-93188-3_1
[Extended version on arXiv:1708.02622]
-
G. Nawratil:
Alternative interpretation of the
Plücker quadric's ambient space and its application.
ICGG 2018 – Proc. of the 18th International Conference on Geometry and Graphics (L. Cocchiarella ed.),
pages 918-929, Springer, 2019, ISBN 978-3-319-95587-2, DOI 10.1007/978-3-319-95588-9_79
[Preprint]
-
G. Nawratil:
Hexapods with plane-symmetric self-motions. In special issue
Kinematics and Robot Design (R. Di Gregorio ed.),
Robotics 7 (2) 27 (2018) DOI 10.3390/robotics7020027 [Open Access]
-
G. Nawratil:
The Plücker Quadric's Ambient Space: Alternative Interpretation and its Application.
Journal for Geometry and Graphics 22 (2) 229-244 (2018)
[Corresponding arXiv paper]
-
A. Rasoulzadeh and G. Nawratil:
Linear Pentapods with a Simple Singularity Variety – Part I: Determination and Redundant Designs.
Advances in Mechanism and Machine Science –
Proc. of the 15th IFToMM World Congress on Mechanism and Machine Science (T. Uhl ed.), pages 689-698, Springer, 2019, ISBN 978-3-030-20131-9,
DOI 10.1007/978-3-030-20131-9_69
[Preprint,
Part of arXiv:1712.06952]
-
A. Rasoulzadeh and G. Nawratil:
Linear Pentapods with a Simple Singularity Variety – Part II: Computation of Singularity-Free Balls.
Advances in Mechanism and Machine Science –
Proc. of the 15th IFToMM World Congress on Mechanism and Machine Science (T. Uhl ed.), pages 699-708, Springer, 2019, ISBN 978-3-030-20131-9,
DOI 10.1007/978-3-030-20131-9_70
[Preprint,
Part of arXiv:1712.06952]
-
Z. Li*, G. Nawratil*, F. Rist and M. Hensel:
Invertible Paradoxic Loop Structures for Transformable Design.
Computer Graphics Forum 39 (2) 261-275 (2020) DOI 10.1111/cgf.13928
[Open Access,
Video]
*joint first author
Project Talks
-
G. Nawratil:
Conference on Geometry: Theory and Applications, Ljubljana June 24-28 2013, Slovenia, Title:
Introducing the theory of bonds for Stewart Gough platforms with self-motions.
[Abstract,
Slides]
-
M. Gallet:
XIV Encuentro de Algebra Computacional y Aplicaciones (EACA 2014), Barcelona June 18-20 2014, Spain, Title:
Bond theory for pentapods and hexapods.
[Extended Abstract]
-
G. Nawratil:
14th International Symposium on Advances in Robot Kinematics (ARK'14), Ljubljana June 29-July 3 2014, Slovenia, paper presentation.
[Slides]
-
G. Nawratil:
16th International Conference on Geometry and Graphics (ICGG'14), Innsbruck August 4-8 2014, Austria, paper presentation.
[Extended Abstract,
Slides]
-
G. Nawratil:
Conference on Geometry: Theory and Applications, Kefermarkt June 8-12 2015, Austria, Title:
Fundamentals of quaternionic kinematics in Euclidean 4-space.
[Abstract,
Slides]
-
M. Gallet:
Effective Methods in Algebraic Geometry (MEGA 2015), Trento June 15-19 2015, Italy, Title:
Construction of movable hexapods via Möbius photogrammetry.
[Abstract]
-
G. Nawratil:
2. IFToMM D-A-CH Konferenz, Innsbruck February 25-26 2016, Austria, Title:
Kinematische Abbildungen für die Menge orientierter Linienelemente.
-
G. Nawratil:
Workshop on geometric rigidity and applications, Edinburgh May 30-June 3 2016, Scotland, Title:
A necessary geometric criterion for the mobility of n-pods.
[Slides]
-
G. Nawratil:
15th International Symposium on Advances in Robot Kinematics (ARK'16), Grasse June 26-30 2016, France, paper presentation.
[Slides]
-
G. Nawratil:
6th European Conference on Mechanism Science (EuCoMeS), Nantes September 20-23 2016, France, paper presentation.
[Slides]
-
G. Nawratil:
7th IFToMM International Workshop on Computational Kinematics (CK), Futuroscope-Poitiers May 22-24 2017, France, paper presentation.
[Slides]
-
A. Rasoulzadeh:
7th IFToMM International Workshop on Computational Kinematics (CK), Futuroscope-Poitiers May 22-24 2017, France, paper presentation.
-
G. Nawratil:
Conference on Geometry: Theory and Applications, Pilsen June 26-30 2017, Czech Republic, Title:
On the set of oriented line-elements: point-models, metrics and applications.
[Abstract,
Slides]
-
G. Nawratil:
12th IFToMM International Symposium on Science of Mechanisms and Machines (SYROM'2017), Iasi November 2-3 2017, Romania,
Plenary Talk, Title: Kinematically Redundant Octahedral Motion Platform for Virtual Reality Simulations.
-
A. Rasoulzadeh:
4. IFToMM D-A-CH Konferenz, Lausanne February 15-16 2018, Switzerland, Title:
Lineare Pentapoden mit einfacher Singularitätsvarietät.
[Abstract]
-
G. Nawratil:
16th International Symposium on Advances in Robot Kinematics (ARK'18), Bologna July 1-5 2018, Italy, paper presentation.
[Slides]
-
G. Nawratil:
18th International Conference on Geometry and Graphics (ICGG'18), Milano August 3-7 2018, Italy, paper presentation.
[Extended Abstract,
Slides]
-
G. Nawratil:
39. Fortbildungstagung für Geometrie,
Strobl November 8-10 2018, Austria, Title: Symmetric Rollings with Spherical Trajectories.
[Abstract,
Slides]
-
A. Rasoulzadeh: 15th IFToMM World Congress,
Krakow June 30-July 4 2019, Poland, paper presentations.
-
Z. Li: Eurographics & Eurovis,
Norrköping May 25-29 2020, Sweden, virtual paper presentation (due to COVID-19).
[Talk on YouTube,
Slides]
|

 Technische Universität Wien
Technische Universität Wien
